【閱讀材料】
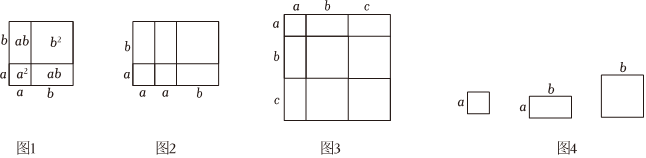
“數形結合”是一種非常重要的數學思想方法．比如：北師大版七年級下冊教材在學習“完全平方公式”時，通過構造幾何圖形，用幾何直觀的方法解釋了完全平方公式：（a+b）2=a2+2ab+b2 （如圖1）．利用“數形結合”的思想方法，可以從代數角度解決圖形問題，也可以用圖形關系解決代數問題．
【方法應用】
根據以上材料提供的方法，完成下列問題：
（1）由圖2可得等式：（2a+b）（a+b）=2a2+b2+3ab（2a+b）（a+b）=2a2+b2+3ab；由圖3可得等式：（a+b+c）2=a2+b2+c2+2ab+2ac+2bc（a+b+c）2=a2+b2+c2+2ab+2ac+2bc；
（2）利用圖3得到的結論，解決問題：若a+b+c=15，ab+ac+bc=35，則a2+b2+c2= 155155；
（3）如圖4，若用其中x張邊長為a的正方形，y張邊長為b的正方形，z張邊長分別為a,b的長方形紙片拼出一個面積為（2a+b）（a+2b）長方形（無空隙、無重疊地拼接）．
①請畫出拼出后的長方形；
②x+y+z= 99；
（4）如圖4，若有3張邊長為a的正方形紙片，4張邊長分別為a,b的長方形紙片，5張邊長為b的正方形紙片．從中取出若干張紙片，每種紙片至少取一張．把取出的這些紙片拼成一個正方形（無空隙、無重疊地拼接），則拼成的正方形的邊長最長可以為 a+2ba+2b．
【答案】（2a+b）（a+b）=2a2+b2+3ab；（a+b+c）2=a2+b2+c2+2ab+2ac+2bc；155；9；a+2b
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：589引用：2難度：0.4
相似題
-
1．設a、b為任意不相等的正數，且
，x=b2+4a，則x、y一定（ ）y=a2+4b發布：2025/5/25 18:30:1組卷：50引用：1難度：0.6 -
2．正實數x、y、z滿足：xy+3yz=20，則2x2+5y2+2z2的最小值為 ．
發布：2025/5/25 19:30:2組卷：86引用：1難度：0.5 -
3．一個四位正整數P滿足千位上的數字比百位上的數字大2，十位上的數字比個位上的數字大2，千位上的數字與十位上的數字不相等且各個數位上的數字均不為零，則稱P為“雙減數”，將“雙減數”P的千位和十位數字組成的兩位數與百位和個位數字組成的兩位數的和記為M（P），將“雙減數”P的千位和百位數字組成的兩位數與十位和個位數字組成的兩位數的差記為N（P），并規定F（P）=
．M（P）N（P）
例如：四位正整數7564，∵7-5=6-4=2，且7≠6，∴7564是“雙減數”，此M（7564）=76+54=130，N（7564）=75-64=11，∴F（7564）=．13011
（1）填空：F（3186）=，并證明對于任意“雙減數”A，N（A）都能被11整除；
（2）若“雙減數”P為偶數，且M（P）-N（P）能被6整除，求滿足條件的所有“雙減數”P，并求F（P）的值．發布：2025/5/25 17:0:1組卷：383引用：2難度：0.5