如圖，在海岸線EF一側有一休閑游樂場，游樂場的前一部分邊界為曲線段FGBC，該曲線段是函數y=Asin（ωx+φ）（A＞0，ω＞0，φ∈（0，π）），x∈[-4，0]的圖象，圖象的最高點為B（-1，2）．邊界的中間部分為長1千米的直線段CD，且CD∥EF．游樂場的后一部分邊界是以O為圓心的一段圓弧?DE．
（1）求曲線段FGBC的函數表達式；
（2）曲線段FGBC上的入口G距海岸線EF最近距離為1千米，現準備從入口G修一條筆直的景觀路到O，求景觀路GO長；
（3）如圖，在扇形ODE區域內建一個平行四邊形休閑區OMPQ，平行四邊形的一邊在海岸線EF上，一邊在半徑OD上，另外一個頂點P在圓弧?DE上，且∠POE=θ，求平行四邊形休閑區OMPQ面積的最大值及此時θ的值．
?
DE
?
DE
【考點】三角函數應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/10 7:0:2組卷：331引用：6難度：0.5
相似題
-
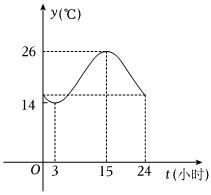1．長春某日氣溫y（℃）是時間t（0≤t≤24，單位：小時）的函數，該曲線可近似地看成余弦型函數y=Acos（ωt+φ）+b的圖象．
（1）根據圖像，試求y=Acos（ωt+φ）+b（A＞0，ω＞0，0＜φ＜π）的表達式；
（2）大數據統計顯示，某種特殊商品在室外銷售可獲3倍于室內銷售的利潤，但對室外溫度要求是氣溫不能低于23℃．根據（1）中所得模型，一個24小時營業的商家想獲得最大利潤，應在什么時間段（用區間表示）將該種商品放在室外銷售，單日室外銷售時間最長不能超過多長時間？（忽略商品搬運時間及其它非主要因素，理想狀態下！）發布：2024/12/29 7:30:2組卷：45引用：4難度：0.5 -
2．筒車是我國古代發明的一種水利灌溉工具，既經濟又環保．明朝科學家徐光啟在《農政全書》中用圖畫描繪了筒車的工作原理（圖1）．假定在水流量穩定的情況下，筒車上的每一個盛水筒都做勻速圓周運動如圖2，將筒車抽象為一個半徑為R的圓，設筒車按逆時針方向每旋轉一周用時120秒，當t=0時，盛水筒M位于點
，經過t秒后運動到點P（x,y），點P的縱坐標滿足y=f（t）=Rsin（ωt+φ）（t≥0，ω＞0，|φ|＜P0（3，-33）），則當筒車旋轉100秒時，盛水筒M對應的點P的縱坐標為 ．π2
發布：2024/12/29 7:0:1組卷：129引用：3難度：0.7 -
3．某實驗室白天的溫度f（t）（單位：℃）隨時間t（單位：h）的變化近似滿足函數關系：
，t∈[6，18]．f（t）=10-2sin（π12t+π3）
（1）求實驗室白天的最大溫差；
（2）若要求實驗室溫度高于11℃，則在哪段時間實驗室需要降溫？發布：2024/12/29 9:0:1組卷：149引用：3難度：0.7