截長補短法在初中數學中有著重要的作用，它主要是用來證線段的和差問題．截長就是在較長的線段上截取一段等于要證的兩段較短的線段中的一段．證剩下的那一段等于另外一段較短的線段．已知點O是線段AB垂直平分線l上的一個動點，以BO為邊作等邊△BOC，點C在直線AB的上方且在直線l的右側，連接AC交直線l于點D，連接BD．
（1）如圖1，點O在線段AB上，請直接用等式表示線段OD，BD，CD之間的數量關系：BD=OD+CDBD=OD+CD；
（2）若點O在線段AB的上方，連接AO，且滿足∠ABO≠30°．如圖2，當∠ABO＜30°時，請探究線段OD，BD，CD之間的數量關系，并說明理由．
【答案】BD=OD+CD
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/18 8:0:9組卷：309引用：2難度：0.5
相似題
-
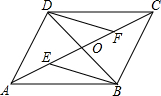1．如圖，四邊形ABCD的對角線AC、BD交于點O，已知O是AC的中點，AE=CF，DF∥BE．
（1）求證：△BOE≌△DOF；
（2）若OD=AC，則四邊形ABCD是什么特殊四邊形？請證明你的結論．12發布：2025/6/18 22:0:2組卷：874引用：70難度：0.5 -
2．如圖，在四邊形ABCD中，AB=AD，CB=CD，AC與BD相交于O點，OC=OA，若E是CD上任意一點，連接BE交AC于點F，連接DF．
（1）證明：△CBF≌△CDF；
（2）若AC=2，BD=2，求四邊形ABCD的周長；3
（3）請你添加一個條件，使得∠EFD=∠BAD，并予以證明．發布：2025/6/18 22:30:2組卷：909引用：63難度：0.1 -
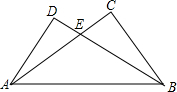3．如圖，在△ABC和△ABD中，AC與BD相交于點E，AD=BC，∠DAB=∠CBA，求證：AC=BD．發布：2025/6/18 22:30:2組卷：1529引用：78難度：0.7