問題探究
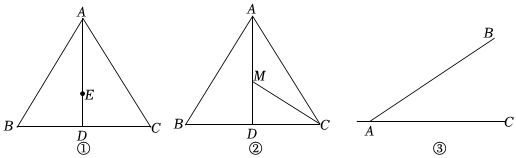
（1）如圖（1），點E是正△ABC高AD上的一定點，請在AB上找一點F，使EF=12AE，并說明理由；
（2）如圖（2），點M是邊長為2的正△ABC高AD上的一動點，求12AM+MC的最小值；
問題解決
（3）如圖（3），A、B兩地相距300km,AC是筆直地沿東西方向向兩邊延伸的一條鐵路．點B到AC的最短距離為180km.今計劃在鐵路線AC上修一個中轉(zhuǎn)站M，再在BM間修一條筆直的公路．如果同樣的物資在每千米公路上的運費是鐵路上的兩倍．那么，為使通過鐵路由A到M再通過公路由M到B的總運費達(dá)到最小值，請確定中轉(zhuǎn)站M的位置，并求出AM的長．（結(jié)果保留根號）
1
2
AE
1
2
AM
+
MC
【考點】三角形綜合題．
【答案】（1）見解析；
（2）；
（3）M點見解析，AM=（240-60）km．
（2）
3
（3）M點見解析，AM=（240-60
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/7 8:0:9組卷：60引用：1難度：0.4
相似題
-
1．閱讀材料，解決問題．
相傳古希臘畢達(dá)哥拉斯學(xué)派的數(shù)學(xué)家經(jīng)常在沙灘上研究數(shù)學(xué)問題．他們在沙灘上畫點或用小石子來表示數(shù)，比如，他們研究過1、3、6、10…，由于這些數(shù)可以用圖中所示的三角點陣表示，他們就將每個三角點陣中所有的點數(shù)和稱為三角數(shù)．
則第n個三角數(shù)可以用1+2+3+…+（n-2）+（n-1）+n=（n≥1且為整數(shù)）來表示．n（n+1）2
（1）若三角數(shù)是55，則n=；
（2）把第n個三角點陣中各行的點數(shù)依次換為2，4，6，…，2n,…，請用含n的式子表示前n行所有點數(shù)的和；
（3）在（2）中的三角點陣中前n行的點數(shù)的和能為120嗎？如果能，求出n,如果不能，請說明理由．發(fā)布：2025/5/22 2:0:8組卷：122引用：4難度：0.4 -
2．如圖a和圖b,在△ABC中，AB=AC，BC=8，tanC=
．點K在AC邊上，點M，N分別在AB，BC上，且AM=CN=2．點P從點M出發(fā)沿折線勻速移動，到達(dá)點N時停止；而點Q在AC邊上隨P移動，且始終保持∠APQ=∠B．34
（1）當(dāng)點P在BC上時，求點P與點A的最短距離：
（2）若點P在MB上，且PO將△ABC的面積分成上下4：5兩部分時，求MP的長；
（3）設(shè)點P移動的路程為x,當(dāng)0≤x≤3及3≤x≤9時，分別求點P到直線AC的距離（用含x的式子表示）；
（4）在點P處設(shè)計并安裝一掃描器，按定角∠APQ掃描△APQ區(qū)域（含邊界），掃描器隨點P從M到B再到N共用時36秒．若AK=，請直接寫出點K被掃描到的總時長．94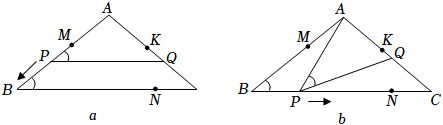
發(fā)布：2025/5/21 18:0:1組卷：138引用：1難度：0.2 -
3．【初步感知】（1）如圖1，點A，B，C，D均在小正方形網(wǎng)格的格點上，則
=；tan∠BAC2
【問題解決】（2）求tan15°的值；
方案①：如圖2，在△ABC中，∠C=90°，∠BAC=30°，作AD平分∠BAC交BC于D；…
方案②：如圖3，在△ABC中，AB=AC，∠A=30°，過點B作BD⊥AC，垂足為D；…
請你選擇其中一種方案求出tan15°的值（結(jié)果保留根號）；
【思維提升】（3）求sin18°的值；如圖4，在△ABC中，AB=AC，∠A=36°．求sin18°的值（結(jié)果保留根號）．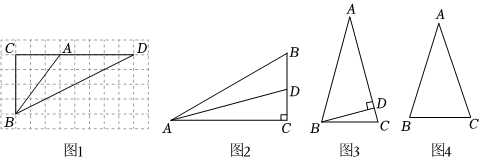
發(fā)布：2025/5/21 20:30:1組卷：350引用：4難度：0.1