如圖，△ABC和△AMN均為等邊三角形，將△AMN繞點A旋轉（△AMN在直線AC的右側）．
（1）求證：△BAM≌△CAN；
（2）若點C，M，N在同一條直線上，
①求∠BMC的度數；
②點M是CN的中點，求證：BM⊥AC．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：2824引用：9難度：0.3

相似題

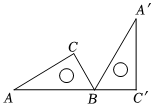1．如圖，將三角尺ABC（∠A=30°，∠C=90°）繞點B按順時針方向轉動一個角度到△A'BC'的位置，若點A、B、C'在同一條直線上，那么旋轉的角度可以是（　　）
A．30° B．60° C．90° D．120°
發布：2025/6/8 21:0:2組卷：68引用：1難度：0.7
解析
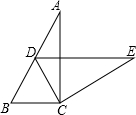2．如圖，在Rt△ABC中，∠ACB=90°，∠A=20°，將△ABC繞點C按順時針方向旋轉后得到△EDC，此時點D在AB邊上，旋轉角為

°．
發布：2025/6/8 21:0:2組卷：297引用：7難度：0.9
解析
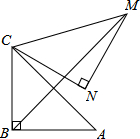3．如圖，在Rt△ABC中，∠ABC=90°，AB=BC=
2
，將△ABC繞點C逆時針旋轉60°，得到△MNC，連接BM，則BM的長是（　　）
A．4 B．
3
+
1
C．
3
+
2
D．
7
發布：2025/6/8 19:0:1組卷：1980引用：11難度：0.7
解析

相關試卷

如圖，△ABC和△AMN均為等邊三角形，將△AMN繞點A旋轉（△AMN在直線AC的右側）．（1）求證：△BAM≌△CAN；（2）若點C，M，N在同一條直線上，①求∠BMC的度數；②點M是CN的中點，求證：BM⊥AC．