2022-2023學年江西省南昌市青山湖區五校聯考九年級（上）期末數學試卷

一、選擇題（本題共6小題，每題3分，共18分）

• 1．若x=2是一元二次方程x²-3x+a=0的一個根，則a的值是（　　）

  A．2

  B．-2

  C．1

  D．-1
  組卷：303引用：3難度：0.8

  解析

• 2．在公園的O處附近有E、F、G、H四棵樹，位置如圖所示（圖中小正方形的邊長均相等）現計劃修建一座以O為圓心，OA為半徑的圓形水池，要求池中不留樹木，則E、F、G、H四棵樹中需要被移除的為（　　）
  

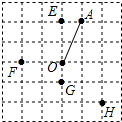
  A．E、F、G

  B．F、G、H

  C．G、H、E

  D．H、E、F
  組卷：3172引用：19難度：0.7

  解析

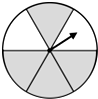• 3．如圖，一個圓形轉盤被分成6個圓心角都為60°的扇形，任意轉動這個轉盤1次，當轉盤停止轉動時，指針指向陰影區域的概率是（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  組卷：853引用：66難度：0.9

  解析

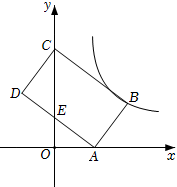• 4．如圖，在平面直角坐標系中，矩形ABCD的頂點A，C分別在x軸，y軸的正半軸上，已知邊AD的中點E在y軸上，且∠DAO=30°，AD=4，若反比例函數

  y

  =

  k

  x

  （k＞0，x＞0）的圖象經過點B，則k的值為（　　）

  A． 8 3

  B．8

  C．6

  D． 6 3
  組卷：1502引用：6難度：0.4

  解析

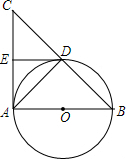• 5．如圖所示，AB是⊙O的直徑，⊙O交BC的中點于D，DE⊥AC于E，連接AD，則下列結論：①AD⊥BC；②∠EDA=∠B；③OA=

  1

  2

  AC；④DE是⊙O的切線，正確的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：1601引用：10難度：0.7

  解析

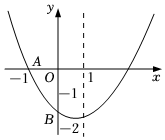• 6．如圖，已知二次函數y=ax²+bx+c（a≠0））的圖象與x軸交于點A（-1，0），與y軸的交點B在（0，-2）和（0，-1）之間（不包括這兩點），對稱軸為直線x=1．下列結論：①abc＞0；②4a+2b+c＞0；③4ac-b²＜8a；④

  1

  3

  ＜

  a

  ＜

  2

  3

  ；⑤b＞c.其中含所有正確結論的選項是（　　）

  A．①③

  B．①③④

  C．②④⑥

  D．①③④⑤
  組卷：354引用：5難度：0.7

  解析

二、填空題（本題共6小題，每題3分，共18分）

• 7．拋物線y=ax²與y=x²的開口大小、形狀一樣、開口方向相反，則a=

   

  ．
  組卷：635引用：7難度：0.7

  解析

五、（本大題共2小題，每小題9分，共18分）

• 22．如圖，拋物線

  y

  =

  -

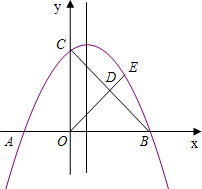  1

  2

  x

  2

  +

  bx

  +

  c

  與x軸交于A、B兩點，與y軸交于點C，且OA=2，OC=3．
  （1）求拋物線的解析式；
  （2）作Rt△OBC的高OD，延長OD與拋物線在第一象限內交于點E，求點E的坐標；
  （3）①在x軸上方的拋物線上，是否存在一點P，使四邊形OBEP是平行四邊形？若存在，求出點P的坐標；若不存在，請說明理由；
  ②在拋物線的對稱軸上，是否存在上點Q，使得△BEQ的周長最小？若存在，求出點Q的坐標；若不存在，請說明理由．
  組卷：3488引用：8難度：0.1

  解析

六、（本大題共12分）

• 23．閱讀下面材料，并解決問題：
  （1）如圖①等邊△ABC內有一點P，若點P到頂點A、B、C的距離分別為3，4，5，求∠APB的度數．
  為了解決本題，我們可以將△ABP繞頂點A旋轉到△ACP′處，此時△ACP′≌△ABP，這樣就可以利用旋轉變換，將三條線段PA、PB、PC轉化到一個三角形中，從而求出∠APB=

  ；
  （2）基本運用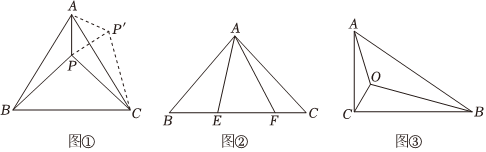
  
  請你利用第（1）題的解答思想方法，解答下面問題
  已知如圖②，△ABC中，∠CAB=90°，AB=AC，E、F為BC上的點且∠EAF=45°，求證：EF²=BE²+FC²；
  （3）能力提升
  如圖③，在Rt△ABC中，∠ACB=90°，AC=1，∠ABC=30°，點O為Rt△ABC內一點，連接AO，BO，CO，且∠AOC=∠COB=∠BOA=120°，求OA+OB+OC的值．
  組卷：12860引用：44難度：0.5

  解析