在小學(xué)我們學(xué)習(xí)過:對(duì)于一個(gè)整數(shù),如果它的各個(gè)數(shù)位上的數(shù)字和可以被3整除,那么這個(gè)數(shù)就一定能夠被3整除
(1)請(qǐng)你判斷112233 能能(填能或不能)被3整除;
(2)為什么可以用各數(shù)位上的數(shù)字之和判斷一個(gè)數(shù)能不能被3整除呢?小明先選了一個(gè)能被3整除的四位數(shù)“1326”試著進(jìn)行推理:
| 1326=1000×1+100×3+10×2+1×6=(999+1)×1+(99+1)×3+(9+1)×2+6=999×1+99×3+9×2+(1+3+2+6) ∵“3(333×1+33×3+3×2)”能被3整除, ∴當(dāng)“1+3+2+6”能被3整除,原數(shù)就能被3整除. |
abcd
abcd
(3)定義:一個(gè)自然數(shù)按從右往左的第1、3、5、7、…數(shù)位,我們稱為奇位,按從右往左的第2、4、6、8、…數(shù)位,我們稱為偶位,例如:一個(gè)四位數(shù),其個(gè)位與百位即奇位,十位與千位為偶位.奇位和就是把所有位于奇位上的數(shù)字相加,偶位和就是把所有位于偶位上的數(shù)字相加.請(qǐng)證明,若
abcd
abcd
【考點(diǎn)】規(guī)律型:數(shù)字的變化類;數(shù)的整除.
【答案】能
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/11 8:0:9組卷:134引用:3難度:0.5
相似題
-
1.已知:a是不為1的有理數(shù),我們把
稱為a的差倒數(shù).如:5的差倒數(shù)是11-a,-3的差倒數(shù)是11-5=-14,已知11-(-3)=14,a2是a1的差倒數(shù),a3是a2的差倒數(shù),a4是a3的差倒數(shù),…,以此類推,a2020的值為( )a1=32A.-2 B. 13C. 23D. 32發(fā)布:2025/6/21 13:0:29組卷:104引用:3難度:0.6 -
2.一列數(shù)按某規(guī)律排列如下
,…若第n個(gè)數(shù)為11,12,21,13,22,31,14,23,32,41,則n=.56發(fā)布:2025/6/21 12:0:1組卷:1487引用:3難度:0.3 -
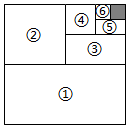 3.如圖,將一個(gè)邊長(zhǎng)為1的正方形紙片分割成7個(gè)部分,部分1是邊長(zhǎng)為1的正方形紙片面積的一半,部分2是部分1面積的一半,部分3是部分2面積的一半,依此類推.陰影部分的面積是 ;受此啟發(fā),則+12+14+…+18的值為 .126發(fā)布:2025/6/21 12:0:1組卷:974引用:3難度:0.8
3.如圖,將一個(gè)邊長(zhǎng)為1的正方形紙片分割成7個(gè)部分,部分1是邊長(zhǎng)為1的正方形紙片面積的一半,部分2是部分1面積的一半,部分3是部分2面積的一半,依此類推.陰影部分的面積是 ;受此啟發(fā),則+12+14+…+18的值為 .126發(fā)布:2025/6/21 12:0:1組卷:974引用:3難度:0.8


