工人師傅有一塊不規則的模板，他已經在模板上畫出了一條裁割線AB，現根據木板的情況，需要通過AB上一點C，作AB的垂線，進行裁割，但手頭沒有直角尺，怎么辦呢？
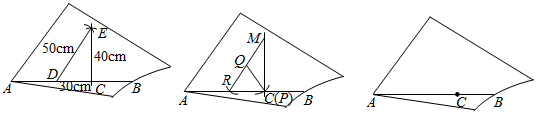
方法一：如圖1，取卷尺在AB上量出CD=30cm,然而分別以D，C為圓心，以50cm與40cm為半徑畫圓弧，兩弧相交于點E，作直線CE，則∠DCE=90°；
方法二：如圖2，在繩子EF上割取任意長度a,一端記點P，另一端記為點Q，將P點與C點重合，按如圖位置擺放，然后以Q為圓心，PQ的長為半徑畫弧，交AB于點R，連接RQ，并延長到點M使得QM=QR，連接CM，則∠MCR=90°．
任務：（1）方法一依據的數學原理是 勾股定理的逆定理勾股定理的逆定理．
（2）利用方法2，證明∠MCR=90°；
（3）方法三，尺規作圖：如圖3，請在木板上，過點C作出AB的垂線l（保留作圖痕跡，不寫作法）．
【考點】三角形綜合題．
【答案】勾股定理的逆定理
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/6 3:0:8組卷：81引用：1難度：0.5
相似題
-
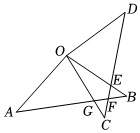1．如圖，△AOB中，OA=OB=6，將△AOB繞點O逆時針旋轉得到△COD．OC與AB交于點G，CD分別交OB、AB于點E、F．
（1）∠A與∠D的數量關系是：∠A ∠D；
（2）求證：△AOG≌△DOE；
（3）當A，O，D三點共線時，恰好OB⊥CD，求此時CD的長．發布：2025/5/25 10:0:1組卷：82引用：1難度：0.2 -
2．如圖，△ABC中，∠ACB=90°，CB=CA，CE⊥AB于E，點F是CE上一點，連接AF并延長交BC于點D，CG⊥AD于點G，連接EG．
（1）求證：CD2=DG?DA；
（2）如圖1，若點D是BC中點，求證：CF=2EF；
（3）如圖2，若GC=2，GE=2，求證：點F是CE中點．2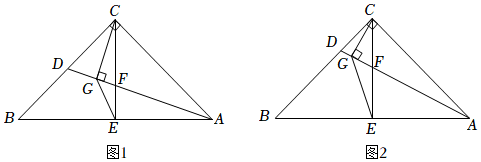
發布：2025/5/25 11:0:2組卷：265引用：2難度：0.1 -
3．【閱讀理解】
截長補短法，是初中數學幾何題中一種輔助線的添加方法．截長就是在長邊上截取一條線段與某一短邊相等，補短是通過在一條短邊上延長一條線段與另一短邊相等，從而解決問題．
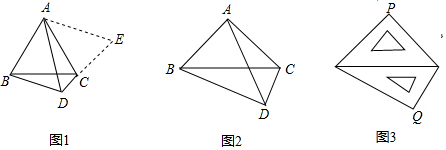
（1）如圖1，△ABC是等邊三角形，點D是邊BC下方一點，∠BDC=120°，探索線段DA、DB、DC之間的數量關系．
解題思路：延長DC到點E，使CE=BD，連接AE，根據∠BAC+∠BDC=180°，可證∠ABD=∠ACE易證得△ABD≌△ACE，得出△ADE是等邊三角形，所以AD=DE，從而探尋線段DA、DB、DC之間的數量關系．
根據上述解題思路，請直接寫出DA、DB、DC之間的數量關系是 ；
【拓展延伸】
（2）如圖2，在Rt△ABC中，∠BAC=90°，AB=AC．若點D是邊BC下方一點，∠BDC=90°，探索線段DA、DB、DC之間的數量關系，并說明理由；
【知識應用】
（3）如圖3，兩塊斜邊長都為14cm的三角板，把斜邊重疊擺放在一起，則兩塊三角板的直角頂點之間的距離PQ的長為 cm.發布：2025/5/25 9:0:1組卷：427引用：6難度：0.3