2022-2023學年江蘇省徐州市鼓樓區樹人中學八年級（上）期中數學試卷
發布：2024/9/6 3:0:8
一、選擇題（本大題共有8小題，每題3分，共2分。在每小題所給出的四個選項中，只有一項是符合題目要求的，請將正確選項的字母代號填寫在答題卡相應的位置）
-
1．現實世界中，對稱現象無處不在，中國的方塊字有些也具有對稱性下列漢字是軸對稱圖形的是（ ）
組卷：94引用：6難度：0.9 -
2．滿足下列條件的△ABC，不是直角三角形的是（ ）
組卷：488引用：17難度：0.9 -
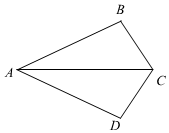3．如圖，已知AB=AD，下列條件中，添加后仍不能判定△ABC≌△ADC的是（ ）組卷：610引用：12難度：0.8 -
4．等腰三角形的底角為50°，則這個等腰三角形的頂角為（ ）
組卷：462引用：9難度：0.9 -
5．如圖，以△ABC的頂點A為圓心，BC的長為半徑作弧；再以頂點C為圓心，AB的長為半徑作弧，兩弧交于點D；連接AD，CD，則△ABC≌△CDA，理由是（ ）組卷：184引用：4難度：0.6 -
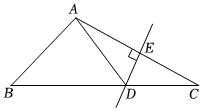6．如圖，△ABC中，DE是AC的垂直平分線，AE=5cm,△ABD的周長為18cm,則△ABC的周長為（ ）組卷：1607引用：12難度：0.9 -
7．《九章算術》中記載：今有戶不知高、廣，竿不知長、短．橫之不出四尺，從之不出二尺，斜之適出．問戶高、廣、斜各幾何？
譯文是：今有門，不知其高、寬，有竿，不知其長、短．橫放，竿比門寬長出4尺；豎放，竿比門高長出2尺；斜放，竿與門對角線恰好相等．問門高、寬、對角線長分別是多少？若設門對角線長為x尺，則可列方程為（ ）組卷：1373引用：23難度：0.5 -
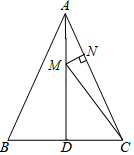8．如圖，△ABC中，AB=AC=13，BC=10，AD是BC邊上的中線，M是AD上的一個動點，作MN⊥AC交AC于N，則CM+MN的最小值為（ ）組卷：1371引用：3難度：0.5
三、解答題
-
24．工人師傅有一塊不規則的模板，他已經在模板上畫出了一條裁割線AB，現根據木板的情況，需要通過AB上一點C，作AB的垂線，進行裁割，但手頭沒有直角尺，怎么辦呢？
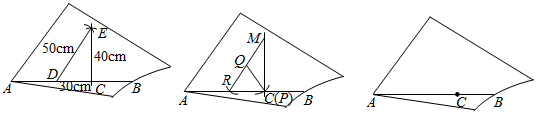
方法一：如圖1，取卷尺在AB上量出CD=30cm,然而分別以D，C為圓心，以50cm與40cm為半徑畫圓弧，兩弧相交于點E，作直線CE，則∠DCE=90°；
方法二：如圖2，在繩子EF上割取任意長度a,一端記點P，另一端記為點Q，將P點與C點重合，按如圖位置擺放，然后以Q為圓心，PQ的長為半徑畫弧，交AB于點R，連接RQ，并延長到點M使得QM=QR，連接CM，則∠MCR=90°．
任務：（1）方法一依據的數學原理是 ．
（2）利用方法2，證明∠MCR=90°；
（3）方法三，尺規作圖：如圖3，請在木板上，過點C作出AB的垂線l（保留作圖痕跡，不寫作法）．組卷：81引用：1難度：0.5 -
25．同學們，等邊三角形、等腰直角三角形都是最常見的幾何圖形．
（1）如圖1，以等邊△ABC的邊BC為腰作等腰直角△BCD，其中∠DBC=90°，BD=CB，點D，點A都在BC同側，延長BD、CA交于點M、連接AD，求∠MAD的度數．
（2）如圖2，在（1）的條件下，作BN平分∠DBC交AC于點N，求證：MD=CN；
（3）如圖3，將圖（1）的△CBD沿著BC翻折得到△CBD1，連接AD1，P為AD1中點，連接BP并延長交CD1于點Q、請猜測CQ、BP、PQ三條線段之間的數量關系，并證明你的結論．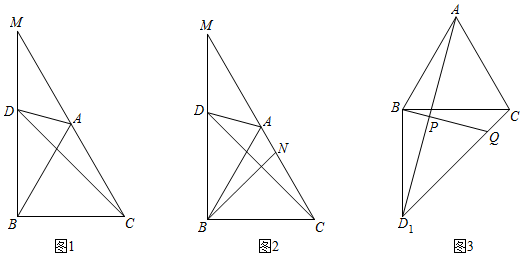
組卷：2054引用：9難度：0.2