閱讀資料:
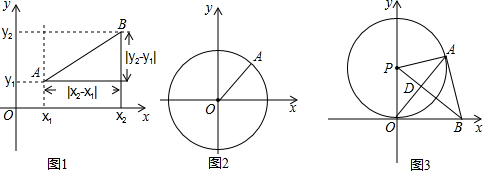
如圖1,在平面直角坐標(biāo)系xOy中,A,B兩點的坐標(biāo)分別為A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B兩點間的距離為AB=(x2-x1)2+(y2-y1)2.
我們知道,圓可以看成到圓心距離等于半徑的點的集合,如圖2,在平面直角坐標(biāo)系xOy中,A(x,y)為圓上任意一點,則A到原點的距離的平方為OA2=|x-0|2+|y-0|2,當(dāng)⊙O的半徑為r時,⊙O的方程可寫為:x2+y2=r2.
問題拓展:如果圓心坐標(biāo)為P(a,b),半徑為r,那么⊙P的方程可以寫為 (x-a)2+(y-b)2=r2(x-a)2+(y-b)2=r2.
綜合應(yīng)用:
如圖3,⊙P與x軸相切于原點O,P點坐標(biāo)為(0,6),A是⊙P上一點,連接OA,使tan∠POA=34,作PD⊥OA,垂足為D,延長PD交x軸于點B,連接AB.
①證明AB是⊙P的切線;
②是否存在到四點O,P,A,B距離都相等的點Q?若存在,求Q點坐標(biāo),并寫出以Q為圓心,以O(shè)Q為半徑的⊙Q的方程;若不存在,說明理由.
(
x
2
-
x
1
)
2
+
(
y
2
-
y
1
)
2
3
4
【考點】圓的綜合題;相似三角形的判定與性質(zhì);銳角三角函數(shù)的定義;等腰三角形的性質(zhì);勾股定理;切線的判定與性質(zhì);全等三角形的判定與性質(zhì);直角三角形斜邊上的中線.
【答案】(x-a)2+(y-b)2=r2
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:923引用:6難度:0.1
相似題
-
1.如圖,已知四邊形ABCD內(nèi)接于⊙O,連接AC、BD,∠ADC+2∠ACD=180°.
(1)求證:BD平分∠ABC;
(2)如圖2,若∠ADB+∠BAC=90°,求證:AB=AC.12
(3)在(2)的條件下,連接DO并延長交⊙O于點E,交AB、AC于點H、K,連接EB,當(dāng)AC=30,BE=11時,求tan∠ABC的值.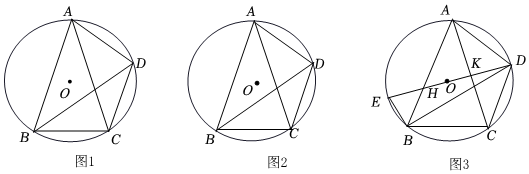 發(fā)布:2025/5/25 15:0:2組卷:245引用:1難度:0.3
發(fā)布:2025/5/25 15:0:2組卷:245引用:1難度:0.3 -
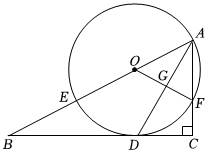 2.如圖,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于點D,O為AB上一點,經(jīng)過點A,D的⊙O分別交AB,AC于點E、F,連接OF交AD于點G.
2.如圖,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于點D,O為AB上一點,經(jīng)過點A,D的⊙O分別交AB,AC于點E、F,連接OF交AD于點G.
(1)求證:BC是⊙O的切線;
(2)求證:AD2=AB?AF;
(3)若BE=8,tanB=,求AD的長.512發(fā)布:2025/5/25 14:0:1組卷:308引用:1難度:0.3 -
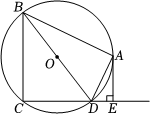 3.如圖,四邊形ABCD內(nèi)接于⊙O,BD是⊙O的直徑,AE⊥CD于點E,DA平分∠BDE.
3.如圖,四邊形ABCD內(nèi)接于⊙O,BD是⊙O的直徑,AE⊥CD于點E,DA平分∠BDE.
(1)求證:AE是⊙O的切線;
(2)如果AB=4,AE=2,求⊙O的半徑.發(fā)布:2025/5/25 16:0:2組卷:2629引用:23難度:0.7
相關(guān)試卷


