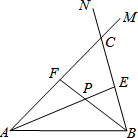
在線段AB的同側作射線AM和BN，若∠MAB與∠NBA的平分線分別交射線BN，AM于點E，F，AE和BF交于點P．如圖，點點同學發現當射線AM，BN交于點C；且∠ACB=60°時，有以下兩個結論：
①∠APB=120°；②AF+BE=AB．
那么，當AM∥BN時：
（1）點點發現的結論還成立嗎？若成立，請給予證明；若不成立，請求出∠APB的度數，寫出AF，BE，AB長度之間的等量關系，并給予證明；
（2）設點Q為線段AE上一點，QB=5，若AF+BE=16，四邊形ABEF的面積為323，求AQ的長．
3
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：2334引用：4難度：0.1
相似題
-
1．在四邊形ABCD中，∠A=∠B=90°，E為AB邊上的點．
（1）連接CE，DE，CE⊥DE；
①如圖1，若AE=BC，求證：AD=BE；
②如圖2，若AE=BE，求證：CE平分∠BCD；
（2）如圖3，F是∠BCD的平分線CE上的點，連接BF，DF，若BC=4，CD=6，，求CF的長．BF=DF=362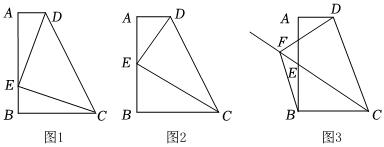
發布：2025/6/7 22:30:2組卷：95引用：2難度：0.1 -
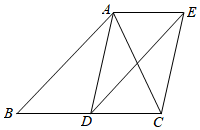2．如圖，點D為△ABC的邊BC的中點，過點A作AE∥BC．且AE=BC，連接DE，CE．12
（1）求證：AD=EC；
（2）若AB=AC，判斷四邊形ADCE的形狀，并說明理由；
（3）若要使四邊形ADCE為正方形．則△ABC應滿足什么條件？
（直接寫出條件即可，不必證明）發布：2025/6/7 21:0:1組卷：166引用：6難度：0.3 -
3．閱讀與應用：同學們：你們已經知道（a-b）2≥0，即a2-2ab+b2≥0．
∴a2+b2≥2ab（當且僅當a=b時取等號）．
閱讀1：若a,b為實數，且a＞0，b＞0，∵（-a）2≥0，∴a-2b+b≥0．ab
∴a+b≥2（當且僅當a=b時取等號）．ab
閱讀2：若函數y=x+（m＞0，x＞0，m為常數），由閱讀1結論可知：mx
x+≥2mx即x+x?mx≥2mx，m
∴當x=，即x2=m,∴x=mx（m＞0）時，函數y=x+m的最小值為2mx．m
閱讀理解上述內容，解答下列問題：
問題1：若函數y=a-1+（a＞1），則a=時，函數y=a-1+16a-1（a＞1）的最小值為 ；16a-1
問題2：已知一個矩形的面積為9cm,求此矩形周長的最小值；
問題3：求代數式（m＞-1）的最小值．m2+2m+10m+1發布：2025/6/7 23:30:2組卷：59引用：1難度：0.2