2016-2017學年浙江省嘉興市海寧市新倉中學九年級（下）開學數學試卷

一、填空題（每題3分）

• 1．二次函數y=x²+2x-3的圖象與y軸的交點坐標是（　　）

  A．（0，-3）

  B．（-3，0）

  C．（1，0）

  D．（0，1）
  組卷：361引用：2難度：0.9

  解析

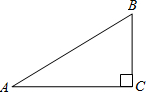• 2．如圖，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，則tanA的值為（　　）

  A．2

  B． 1 2

  C． 5 5

  D． 2 5 5
  組卷：446引用：43難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A．a3+a3=a6

  B．3a-a=3

  C．（a3）2=a5

  D．a?a2=a3
  組卷：1715引用：18難度：0.9

  解析

• 4．一個學習興趣小組有4名女生，6名男生，現要從這10名學生中選出一人擔當組長，則女生當組長的概率是（　　）

  A． 2 5

  B． 3 5

  C． 2 3

  D． 1 2
  組卷：105引用：4難度：0.7

  解析

• 5．如圖，四邊形ABCD內接于半圓O，已知∠ADC=140°，則∠AOC的大小是（　　）

  A．40°

  B．60°

  C．70°

  D．80°
  組卷：1588引用：6難度：0.7

  解析

• 6．將拋物線y=（x-1）²+1向下平移1個單位，所得新拋物線的解析式為（　　）

  A．y=（x-1）2+2

  B．y=（x-1）2

  C．y=（x-2）2+1

  D．y=x2+1
  組卷：115引用：2難度：0.7

  解析

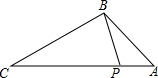• 7．如圖，已知點P在△ABC的邊AC上，下列條件中，不能判斷△ABP∽△ACB的是（　　）

  A．∠ABP=∠C

  B．∠APB=∠ABC

  C．AB2=AP?AC

  D． AB BP = AC CB
  組卷：532引用：4難度：0.7

  解析

• 8．若分式

  x

  -

  2

  x

  +

  3

  的值為0，則x的值是（　　）

  A．-3

  B．-2

  C．0

  D．2
  組卷：1525引用：17難度：0.7

  解析

三、解答題

• 25．從三角形（不是等腰三角形）一個頂點引出一條射線與對邊相交，頂點與交點之間的線段把這個三角形分割成兩個小三角形，如果分得的兩個小三角形中一個為等腰三角形，另一個與原三角形相似，我們把這條線段叫做這個三角形的完美分割線．
  （1）如圖1，在△ABC中，CD為角平分線，∠A=40°，∠B=60°，求證：CD為△ABC的完美分割線．
  （2）在△ABC中，∠A=48°，CD是△ABC的完美分割線，且△ACD為等腰三角形，求∠ACB的度數．
  （3）如圖2，△ABC中，AC=2，BC=

  2

  ，CD是△ABC的完美分割線，且△ACD是以CD為底邊的等腰三角形，求完美分割線CD的長．
  
  組卷：7951引用：40難度：0.3

  解析

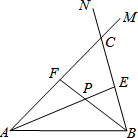• 26．在線段AB的同側作射線AM和BN，若∠MAB與∠NBA的平分線分別交射線BN，AM于點E，F，AE和BF交于點P．如圖，點點同學發現當射線AM，BN交于點C；且∠ACB=60°時，有以下兩個結論：
  ①∠APB=120°；②AF+BE=AB．
  那么，當AM∥BN時：
  （1）點點發現的結論還成立嗎？若成立，請給予證明；若不成立，請求出∠APB的度數，寫出AF，BE，AB長度之間的等量關系，并給予證明；
  （2）設點Q為線段AE上一點，QB=5，若AF+BE=16，四邊形ABEF的面積為32

  3

  ，求AQ的長．
  組卷：2334引用：4難度：0.1

  解析