如圖，在矩形ABCD中，AB=4cm,AD=12cm,P點在AD邊上以每秒1cm的速度從A向D運動，點Q在BC邊上，以每秒4cm的速度從C出發，在C、B間往返運動，兩點同時出發，P點到達D點時同時停止，在這段時間內，有如下說法：
①該過程中，會出現4次PQ∥AB的時刻；
②該過程中，會出現3次四邊形ABQP和四邊形PQCD同時為矩形的時刻；
③該過程中，當t=5時，四邊形ABQP和四邊形PQCD的面積比為65；
④該過程中，矩形ABQP和PQCD面積比的最大值為43．
上述說法正確的是 ①②①②（填序號）
6
5
4
3
【答案】①②
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 14:0:2組卷：29引用：1難度：0.5
相似題
-
1．
閱讀以上材料，完成下列問題：圓冪定理是平面幾何中最重要的定理之一，它包含了相交弦定理、切割線定理、割線定理以及它們推論，其中切割線定理的內容是：從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項．
喜歡思考的天天在了解這個定理之后嘗試給出證明，下面是他的部分證明過程：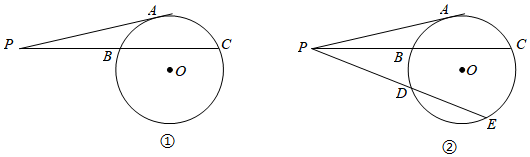
已知：如圖①，點P為⊙O外一點，切線PA與圓相切于點A，割線PBC與圓相交于點B、C．求證：PA2=PB?PC．
證明：如圖，連接AB、AC、BO、AO，
∵PA切⊙O于點A，
∴PA⊥AO，即∠PAB+∠BAO=90°．
…
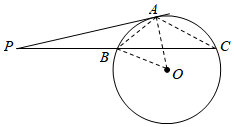
（1）請幫助天天補充完成以上證明過程；
（2）如圖②，割線PDE與圓交于點D、E，且PB=BC=4，PE=7，求DE的長．發布：2025/5/24 19:0:1組卷：711引用：3難度：0.5 -
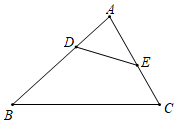2．如圖，在△ABC中，D、E分別為AB、AC邊上的點，且∠AED=∠B，AD=3，AC=6，DB=5，則AE的長度為（ ）發布：2025/5/24 19:30:1組卷：551引用：6難度：0.7 -
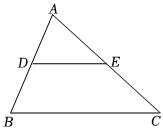3．如圖，在△ABC中，點D，E分別是AB，AC的中點若△ADE的面積是2cm2，則四邊形BDEC的面積為（ ）發布：2025/5/24 19:30:1組卷：103引用：7難度：0.6