我們定義：若一個三角形最大邊上的點將該邊分為兩條線段，且這兩條線段的積等于這個點到最大邊所對頂點連線的平方，則稱這個點為這個三角形的“比例中點”．例如：如圖1，已知鈍角△ABC中，∠ACB是鈍角，點D是AB上的一點，連接CD，若CD2=AD?BD，則稱點D是△ABC的“比例中點”．
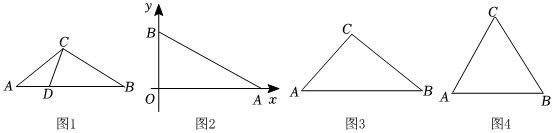
（1）如圖2，已知點A的坐標為（4，0），點B在y軸上，∠BAO=30°，若點M是△AOB的“比例中點”，則點M的坐標為 （1，3）或（2，233）（1，3）或（2，233）；
（2）如圖3，已知△ABC中，AB=28，∠A=45°，tanB=34，若點N是△ABC的“比例中點”，求AN；
（3）如圖4，已知△ABC是等邊三角形，因為等邊三角形的三邊相等，所以其中任意一條邊都可以看成最大邊，試判斷等邊三角形有沒有“比例中點”？說明理由．
（
1
，
3
）
（
2
，
2
3
3
）
（
1
，
3
）
（
2
，
2
3
3
）
tan
B
=
3
4
【考點】相似形綜合題．
【答案】或
（
1
，
3
）
（
2
，
2
3
3
）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：510引用：4難度：0.1
相似題
-
1．【基礎鞏固】
（1）如圖1，在△ABC中，D為BC上一點，連結AD，E為AD上一點，連結CE，若∠BAD=∠ACE，CD=CE，求證：△ABD∽△CAE．
【嘗試應用】
（2）如圖2，在平行四邊形ABCD中，對角線AC、BD交于點O，E為OC上一點，連結BE，∠CBE=∠DCO，BE=DO，若BD=12，OE=5，求AC的長．
【拓展提升】
（3）如圖3，在菱形ABCD中，對角線AC、BD交于點O，E為BC中點，F為DC上一點，連結OE、AF，∠AEO=∠CAF，若，AC=6，求菱形ABCD的邊長．DFFC=53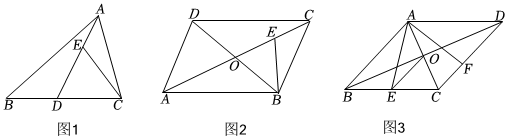
發布：2025/5/21 15:30:1組卷：1433引用：8難度：0.1 -
2．【問題原型】如圖（1）所示，在等腰直角三角形ABC中，∠ACB=90°，BC=a,AB的中點為F，將線段FB繞點B按順時針方向旋轉90得到線段BD，連接CD，過點D作BC邊上的高DE，易證△ABC∽△BDE，從而得到△BCD的面積為
．14a2
【初步探究】如圖（2）所示，在Rt△ABC中，∠ACB=90°，BC=a,AB的中點為F．將線段FB繞點B按順時針方向旋轉90°得到線段BD，連接CD．用含a的代數式表示△BCD的面積，并說明理由．
【簡單應用】如圖（3）所示，在等腰三角形ABC中，AB=AC，BC=a,AB的中點為F．將線段FB繞點B按順時針方向旋轉90°得到線段BD，連接CD，直接寫出△BCD的面積（用含a的代數式表示）．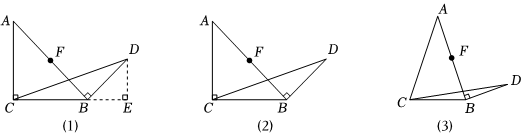
發布：2025/5/21 19:0:1組卷：149引用：1難度：0.2 -
3．在△ABC中，AB=AC=8，
．點D在線段BC上運動（不與點B、C重合）．如圖1，連接AD，作∠ADE=∠B，DE與AC交于點E．tanB=34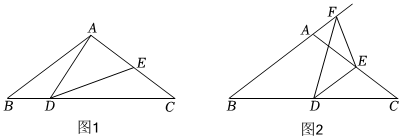
（1）求證：△ABD∽△DCE．
（2）若∠B=40°，當∠ADB為多少度時，△ADE是等腰三角形？
（3）如圖2，當點D運動到BC中點時，點F在BA的延長線上，連接FD，∠FDE=∠B，點E在線段AC上，連接EF．
①△BDF與△DFE是否相似？請說明理由．
②設EF=x,△EDF的面積為S，試用含x的代數式表示S．發布：2025/5/21 18:30:1組卷：296引用：5難度：0.1