[課題學習]：
平行線的“等角轉化”功能．

【閱讀理解]：
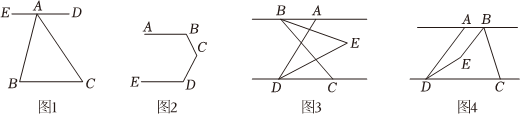
如圖1，已知點A是BC外一點，連接AB，AC，求∠BAC+∠B+∠C的度數．
（1）閱讀并補充下面推理過程．
解：過點A作ED∥BC，所以∠B=

∠EAB

∠EAB

，∠C=

∠DAC

∠DAC

，
又因為∠EAB+∠BAC+∠DAC=180°，
所以∠B+∠BAC+∠C=180°．
[解題反思]：
從上面的推理過程中，我們發現平行線具有“等角轉化”的功能，將∠BAC，∠B，∠C“湊”在一起，得到角的關系，使問題得到解決．
[方法運用]：
（2）如圖2，已知AB∥ED，求∠B+∠BCD+∠D的度數；
[深化拓展]：
（3）已知AB∥CD，點C在D的右側，∠ADC=70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直線交于點E，點E在AB與CD兩條平行線之間．
①如圖3，若∠ABC=60°，則∠BED=

65

65

°．
②如圖4，點B在點A的右側，若∠ABC=n°，則∠BED=

（215-

1

2

n）

（215-

1

2

n）

°（用含n的代數式表示）．