滹沱河岸邊盛開的粉黛亂子草吸引了很多市民前來觀賞，如圖1是其中一處美景的俯視圖，漂亮的粉黛亂子草（扇形EOF中的陰影部分）花開燦爛，已知扇形半徑OE=10米，∠EOF=120°，GN=2.5米，點(diǎn)P為EF的中點(diǎn)，△OEF上有一座供游人休息的亭子（矩形GHMN），點(diǎn)H，G分別在OF，OE上，MN在EF上．
（1）求粉黛亂子草的種植面積；
（2）愛思考的嘉嘉想：“這個矩形亭子的占地面積能否再大一些呢？”請你通過計算回答嘉嘉的問題；
（3）在點(diǎn)P處垂直于地面向上豎著一根高為109米的柱子PA，在A處安裝有一個自動噴水裝置．水流在各個方向上沿拋物線路徑落下，噴出的水流在距離PA的水平距離為23米時達(dá)到最高點(diǎn)．當(dāng)噴頭A旋轉(zhuǎn)時，整個粉黛亂子草剛好都能被噴出的水流覆蓋．建立如圖2的坐標(biāo)系，求出此坐標(biāo)系中拋物線水流對應(yīng)的函數(shù)關(guān)系式．
10
9
3
【考點(diǎn)】二次函數(shù)綜合題．
【答案】（1）（-）（平方米）；
（2）矩形亭子的占地面積不能再大了；
（3）拋物線的表達(dá)式為：y=-（x-2）2+2．
100
π
3
75
3
4
（2）矩形亭子的占地面積不能再大了；
（3）拋物線的表達(dá)式為：y=-
2
27
3
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：79引用：1難度：0.3
相似題
-
1．如圖1，已知二次函數(shù)y=ax2+bx+c（a≠0）的圖象與x軸交于A（-1，0），B（3，0）兩點(diǎn)，與y軸交于點(diǎn)C（0，-3），頂點(diǎn)為D，對稱軸交x軸于點(diǎn)E．
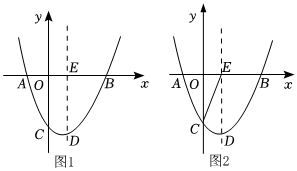
（1）求該二次函數(shù)的解析式；
（2）設(shè)M為直線BC下方拋物線上一點(diǎn)，是否存在點(diǎn)M，使四邊形CMBE面積最大？若存在，請求出點(diǎn)M的坐標(biāo)；若不存在，請說明理由；
（3）連接CE（如圖2），設(shè)點(diǎn)P是位于對稱軸右側(cè)該拋物線上一點(diǎn)，過點(diǎn)P作PQ⊥x軸，垂足為Q．連接PE，請求出當(dāng)△PQE與△COE相似時點(diǎn)P的坐標(biāo)．發(fā)布：2025/5/25 12:30:1組卷：231引用：1難度：0.3 -
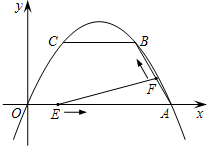2．已知拋物線y=ax2+bx+c經(jīng)過O（0，0），A（4，0），B（3，）三點(diǎn)，連接AB，過點(diǎn)B作BC∥x軸交拋物線于點(diǎn)C．動點(diǎn)E、F分別從O、A兩點(diǎn)同時出發(fā)，其中點(diǎn)E沿線段OA以每秒1個單位長度的速度向A點(diǎn)運(yùn)動，點(diǎn)F沿折線A→B→C以每秒1個單位長度的速度向C點(diǎn)運(yùn)動．設(shè)動點(diǎn)運(yùn)動的時間為t（秒）．3
（1）求拋物線的解析式；
（2）記△EFA的面積為S，求S關(guān)于t的函數(shù)關(guān)系式，并求S的最大值，指出此時△EFA的形狀；
（3）是否存在這樣的t值，使△EFA是直角三角形？若存在，求出此時E、F兩點(diǎn)的坐標(biāo)；若不存在，請說明理由．發(fā)布：2025/5/25 12:30:1組卷：314引用：4難度：0.1 -
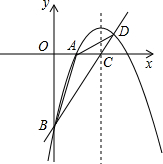3．如圖，已知拋物線y=ax2+4x+c經(jīng)過A（2，0）、B（0，-6）兩點(diǎn)，其對稱軸與x軸交于點(diǎn)C．
（1）求該拋物線和直線BC的解析式；
（2）設(shè)拋物線與直線BC相交于點(diǎn)D，連接AB、AD，求△ABD的面積；
（3）在該拋物線的對稱軸上是否存在點(diǎn)Q，使得△QAB的周長最小？若存在，求出Q點(diǎn)的坐標(biāo)；若不存在，請說明理由．發(fā)布：2025/5/25 12:30:1組卷：143引用：3難度：0.1