探索三角形的內角與外角平分線（三角形的外角是三角形的一邊與另一邊的延長線所組成的角）：
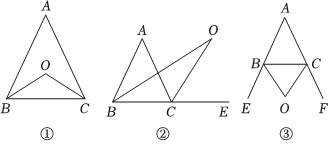
（1）如圖①，在△ABC中，BO平分∠ABC，CO平分∠ACB，若∠A=50°，則∠BOC=115°115°；此時∠A與∠BOC有怎樣的關系？試說明理由；
（2）如圖②，BO平分∠ABC，CO平分∠ACE，若∠A=50°，則∠BOC=25°25°；此時∠A與∠BOC有怎樣的關系？試說明理由；
（3）如圖③，△ABC的外角∠CBE，∠BCF的平分線BO，CO相交于點O，若∠A=50°，則∠BOC=65°65°；此時∠A與∠BOC有怎樣的關系？（不需說明理由）
【考點】三角形綜合題．
【答案】115°；25°；65°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/19 2:0:1組卷：50引用：1難度：0.3
相似題
-
1．定義：由一個三角形的三條中線圍成的三角形稱為原三角形的中線三角形．
問題：設中線三角形的面積為S1，原三角形的面積為S2．求的值．S1S2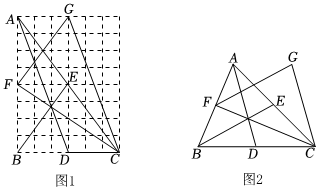
特例探索：
（1）正三角形的邊長為2，則中線長為 ，所以=．S1S2
（2）如圖1，每個小正方形邊長均為1，點A，B，C，D，E，F，G均在網格點上．
①△CFG △ABC的中線三角形．（填“是”或“不是”）
②S△ABC=，S△CFG=，所以=．S1S2
一般情形：
如圖2，△ABC的三條中線分別是AD，BE，CF，將AD平移至CG，連結FG．
（3）求證：△CFG是△ABC的中線三角形；
（4）猜想的值，并說明理由．S1S2發布：2025/5/22 7:30:2組卷：144引用：1難度：0.1 -
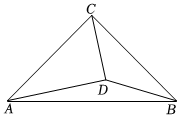2．在△ABC中，∠ACB=90°，AC=BC，點D在△ABC內部，且滿足∠ACD-∠BCD=2∠DAB，若△BCD的面積為13，則CD=．發布：2025/5/22 10:0:1組卷：498引用：3難度：0.3 -
3．【問題提出】
如圖（1），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，點E在△ABC內部，直線AD與BE交于點F．線段AF，BF，CF之間存在怎樣的數量關系？
【問題探究】
（1）如圖（2），當點D，F重合時，
①AF與BE的數量關系是 ．
②=．CFBF-AF
（2）如圖（1），當點D，F不重合時，求的值．CFBF-AF
（3）【問題拓展】
如圖（3），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC（k是常數），點E在△ABC內部，直線AD與BE交于點F，求出線段AF，BF，CF之間的數量關系（用一個含有k的等式表示）．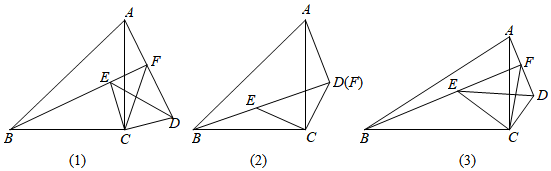
發布：2025/5/22 8:0:2組卷：447引用：2難度：0.2