如圖，在平面直角坐標系中，已知點A，B的坐標分別為A（a,0），B（b,0）．且a,b滿足a+6+（a+b+2）2=0，現將線段AB先向上平移4個單位長度，再向右平移6個單位長度得到線段CD，其中點A對應點為C，點B對應點為D，連接AC，BD．
（1）點C的坐標為 （0，4）（0，4），點D的坐標為 （10，4）（10，4）；
（2）如圖1，點M是線段AC上的一個動點，點N是線段CD的一個定點，連接MN，MO，當點M在線段AC上移動時（不與點A，C重合），請探究∠DNM，∠OMN，∠MOB之間的數量關系，并說明理由；
（3）如圖2，動點P從點O出發，沿y軸正方向以每秒1個單位長度的速度勻速運動，設運動時間為t秒，當S四邊形OBDP＜2S△CDP時，求t的取值范圍．
a
+
6
+
（
a
+
b
+
2
）
2
=
0
【考點】四邊形綜合題．
【答案】（0，4）；（10，4）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：129引用：1難度：0.4
相似題
-
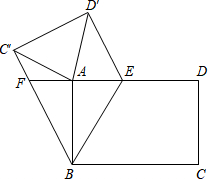1．如圖，在矩形ABCD中，AB=4，AD=6，E是AD邊上的一個動點，將四邊形BCDE沿直線BE折疊，得到四邊形BC′D′E，連接
AC′，AD′．
（1）若直線DA交BC′于點F，求證：EF=BF；
（2）當AE=時，求證：△AC′D′是等腰三角形；433
（3）在點E的運動過程中，求△AC′D′面積的最小值．發布：2025/5/24 17:0:2組卷：632引用：3難度：0.1 -
2．如圖，在平面直角坐標系中有矩形AOBC，AO=6，BO=8，連接OC，點P從頂點A出發以
個單位/秒的速度在線段AC上運動，同時點Q從頂點B出發以1個單位/秒的速度在線段BO上運動，只要有一個點先到達線段的另一個端點時，就停止運動．過點Q作QE⊥OB，交OC于點E，連接PE，設運動時間為t秒．32
（1）當t=2時，tan∠CPE=；
（2）當點P在線段AC．上運動時，設△PEC的面積為S，寫出S關于t的函數表達式，并寫出△PEC的面積最大時點E的坐標；
（3）直接寫出運動中，△PEC為等腰三角形時t的值．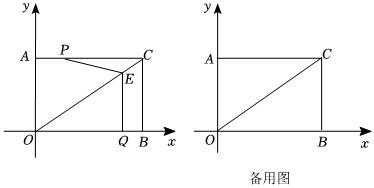
發布：2025/5/24 17:0:2組卷：26引用：1難度：0.1 -
3．如圖（1），已知矩形ABCD中，AB=6cm,BC=
cm,點E為對角線AC上的動點．連接BE．過E作EB的垂線交CD于點F．23
（1）探索BE與EF的數量關系，并說明理由．
（2）如圖（2），過F作AC的垂線交AC于點G，交EB于點H，連接CH．若點E從
A出發沿AC方向以cm/s的速度向終點C運動，設E的運動時間為t s.23
①是否存在t,使得H與B重合？若存在，求出t的值；若不存在，說明理由；
②t為何值時，△CFH是等腰三角形；
③當CG=GH時，求△CGH的面積．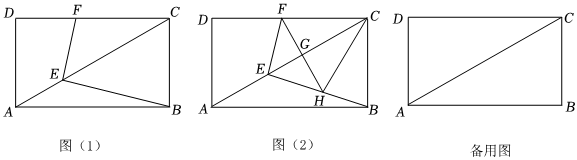
發布：2025/5/24 17:30:1組卷：221引用：1難度：0.2