將二次函數y=-x2+2x+3（0≤x≤4）位于x軸下方的圖象沿x軸向上翻折，與原二次函數位于x軸上方的部分組成一個新圖象，這個新圖象對應的函數最大值與最小值之差為（ ）
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/26 1:30:1組卷：326引用：5難度：0.7
相似題
-
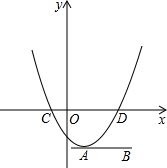1．如圖，點A，點B的坐標分別為（1，-4），（4，-4），拋物線y=a（x-h）2+k的頂點在線段AB上運動，與x軸交于C，D兩點（點C在點D的左側）．若點D的橫坐標的最大值為6，則點C的橫坐標的最小值為（ ）發布：2025/5/26 3:30:1組卷：547引用：3難度：0.5 -
2．已知拋物線y=ax2+4ax-8與直線y=n相交于A，B兩點（點A在點B左側），AB=4，且拋物線與x軸只有一個交點，則n的值為（ ）
發布：2025/5/26 6:30:2組卷：493引用：2難度：0.6 -
3．已知二次函數y=ax2-2ax+c（a≠0）的圖象與x軸的一個交點為（-2，0），則關于x的一元二次方程ax2-2ax+c=0的兩根之積是 ．
發布：2025/5/26 6:30:2組卷：639引用：4難度：0.7