如圖，在平面直角坐標系xOy中，正方形OABC的頂點A，C分別落在x軸，y軸上，點B的坐標為（8，8），點D在線段BC上（不與B，C重合），將△OCD沿OD翻折，使得點C落在同一平面內的點E處．
（1）如圖1，當OD=10時．
①求點D的坐標．
②延長DE交AB于點F，求點F的坐標．
（2）連結BE并延長，交正方形OABC的邊于點G，若BD=OG，求點D的坐標．
【考點】四邊形綜合題．
【答案】（1）①D（6，8）；
②F（8，）；
（2）點D的坐標為（4，8）或（16-8，8）．
②F（8，
8
7
（2）點D的坐標為（4，8）或（16-8
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/6 8:0:9組卷：371引用：2難度：0.3
相似題
-
1．四邊形ABCD是菱形，∠B≤90°，點E為邊BC上一點，聯結AE，過點E作EF⊥AE，EF與邊CD交于點F，且EC=3CF．
（1）如圖1，當∠B=90°時，求S△ABE與S△ECF的比值；
（2）如圖2，當點E是邊BC的中點時，求cosB的值；
（3）如圖3，聯結AF，當∠AFE=∠B且CF=2時，求菱形的邊長．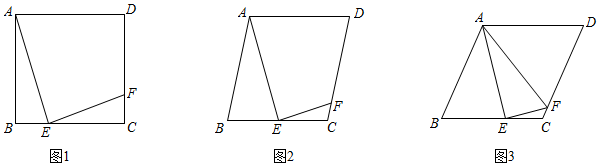
發布：2025/5/22 4:0:7組卷：956引用：3難度：0.2 -
2．【基礎鞏固】：
（1）如圖1，四邊形ABCD中，AC平分∠BAD，AB=AD．
求證：∠ACB=∠ACD；
【遷移運用】：
（2）如圖2，在（1）的條件下，取AB的中點E，連結DE交AC于點F，若∠AFE=∠ACD，，求DF的長；EF=23
【解決問題】：
（3）如圖3，四邊形ABCD中，AD=CD，∠ADC=90°，在BC上取點E，使得DE=DC，恰有BE=AB．若AD=3，CE=6，求四邊形ABCD的面積．10發布：2025/5/22 4:0:7組卷：456引用：3難度：0.4 -
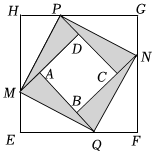3．如圖，4個全等的直角三角形圍出一個正方形ABCD，過點P，Q分別作AC的平行線，過點M，N分別作BD的平行線得四邊形EFGH．若已知正方形ABCD的面積，則直接可求的量是（ ）發布：2025/5/22 4:30:1組卷：514引用：1難度：0.1