【背景知識】數軸是初中數學的一個重要工具，利用數軸可以將數與形完美地結合．研究數軸我們發現了許多重要的規律：若數軸上點A、點B表示的數分別為a、b,則A、B兩點之間的距離AB=|a-b|，線段AB的中點表示的數為a+b2．
【問題情境】如圖1，已知數軸上有三點A、B、C，AB=40，BC=60，點A對應的數是30．
【綜合運用】
（1）點B表示的數是 -10-10，點C表示的數是 -70-70．
（2）如圖2，動點P、Q兩點同時從C、A出發向右運動，同時動點R從點A向左運動，已知點P的速度是點R的速度的4倍，點Q的速度是點R的速度3倍少5個單位長度/秒．經過5秒，點P、Q之間的距離與點Q、R之間的距離相等，求動點Q的速度；
（3）如圖3，O表示原點，動點P、T分別從C、O兩點同時出發向左運動，同時動點R從點A出發向右運動，點P、T、R的速度分別為5個單位長度/秒，1個單位長度/秒、2個單位長度/秒，在運動過程中，如果點M為線段PT的中點，點N為線段OR的中點．請問PT-MN的值是否會發生變化？若不變，請求出相應的數值；若變化，請說明理由．
a
+
b
2
【答案】-10；-70
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：387引用：1難度：0.6
相似題
-
1．（1）在一條長為400米的環形跑道上，甲乙兩人使用不同的交通工具同時不同地出發，都以逆時針方向進行勻速運動，已知甲在第20秒鐘第一次追上乙，第120秒時再次追上乙，甲的速度為每秒13米，求乙的速度．
（2）在一條長為400米的環形跑道上，甲、乙、丙三人使用不同交通工具同時不同地出發，都以逆時針方向進行勻速運動，已知甲在第20秒鐘第一次追上乙，第60秒鐘第一次追上丙，第120秒時再次追上乙，第140秒時再次追上丙，則乙與丙的速度差為 米/秒，乙第一次追上丙用了 秒．發布：2025/6/5 10:0:2組卷：242引用：1難度：0.4 -
2．某商場計劃購進甲，乙兩種節能燈共1200個，這兩種節能燈的進價、售價如下表：
（1）若商場預計進貨款為44000元，則這兩種節能燈應各購買多少個？進價（元/個） 售價 （元/個） 甲型 25 30 乙型 45 60
（2）如何進貨，使銷售完節能燈時，商場獲得的利潤恰好是成本的30%，此時利潤為多少元？發布：2025/6/5 8:30:1組卷：290引用：3難度：0.5 -
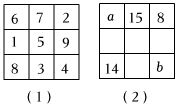3．幻方是古老的數學問題，我國古代的《洛書》中記載了最早的幻方——九宮格．將9個數填入幻方的空格中，要求每一橫行、每一豎列以及兩條對角線上的3個數之和相等，例如圖（1）就是一個幻方．圖（2）是一個未完成的幻方，則a與b的和是（ ）發布：2025/6/5 13:30:2組卷：241引用：3難度：0.6