閱讀下列學習內容：
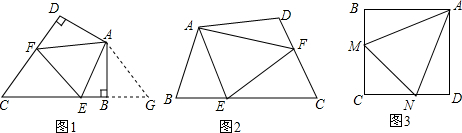
（1）如圖1，在四邊形ABCD中，AB=AD，∠BAD=120°，∠ABC=∠D=90°，E，F分別是BC、CD上的點，且∠EAF=60°，探究圖中線段BE，EF，FD之間的數量關系．
探究思路如下：延長EB到點G，使BG=DF，連接AG．

AB = AD

∠ ABG =∠ D

BG = DF

?△ABG≌△ADF?

∠ GAB =∠ DAF

AG = AF

∠ BAD = 120 °

∠ EAF = 60 °

?∠DAF+∠BAE=60°?∠GAB+∠BAE=60°
∠EAG=60°?

AE = AE

∠ FAE =∠ EAG

AF = AG

?△AEF≌△AEG?EF=EG
則由探究結果知，圖中線段BE、EF、FD之間的數量關系為

EF=BE+FD

EF=BE+FD

．
（2）根據上面的方法，解決問題：
如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，E、F分別是BC、CD上的點，且∠EAF=

1

2

∠BAD，
上述結論是否仍然成立，并說明理由；
（3）如圖3，在四邊形ABCD中，AB=BC=CD=DA，∠BAD=∠B=∠C=∠D=90°，點M、N分別在邊BC、CD上，且∠MAN=45°，若BM=3，ND=2，請求出線段MN的長度．