閱讀以下材料，并按要求完成相應的任務．
《數學的發現》是2006年科學出版社出版的圖書，作者是（美）喬治?波利亞．本書通過對各種類型生動而有趣的典型問題（有些是非數學的））進行細致剖析，提出它們的本質特征，從而總結出各種數學模型．
共高三角形：有一條公共高的三角形稱為共高三角形．
共高定理：如圖①，設點M在直線AB上，點P為直線外一點，則有S△PAMS△PBM=AMBM．
下面是該結論的證明過程：證明：如圖①，過點P作PQ⊥AB于點Q，
……
按要求完成下列任務：
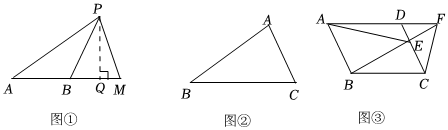
（1）請你按照以上證明思路，結合圖①完成剩余的證明；
（2）如圖②，△ABC，
①畫出∠BAC的平分線（不寫畫法，保留作圖痕跡，使用2B鉛筆作圖）；
②若∠BAC的平分線交BC于D，求證：ABAC=BDCD．
（3）如圖③，E是平行四邊形ABCD邊CD上一點，連接BE并延長，交AD的延長線于點F，連接AE，CF，若△ADE的面積為2，則△CEF的面積為 22．
S
△
PAM
S
△
PBM
=
AM
BM
AB
AC
=
BD
CD
【考點】相似形綜合題．
【答案】2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：193引用：3難度：0.1
相似題
-
1．如圖，四邊形ABCD中，AD∥BC．
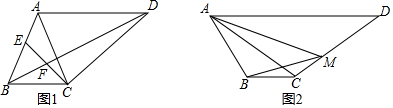
（1）如圖1，AB=AC，點E為AB上一點，∠BEC=∠ACD．
①求證：AB?BC=AD?BE；
②連接BD交CE于F，試探究CF與CE的數量關系，并證明；
（2）如圖2，若AB≠AC，點M在CD上，cos∠DAC=cos∠BMA=，AC=CD=3MC，AD?BC=12，直接寫出BC的長．34發布：2025/5/22 15:30:1組卷：1070引用：3難度：0.1 -
2．如圖1，在正方形ABCD中，點E、F分別在BC、CD上，且BE=DF，AE、AF分別與BD交于點G、H，過點G作GN⊥AF，垂足為M，交AD于點N．
（1）求證：AH=GN；
（2）若∠EAF=45°，求證：；AHAF=BGCF
（3）如圖2，過點G作GQ⊥AD，垂足為Q，交AF于點P，若GM=2MN，求的值．APGP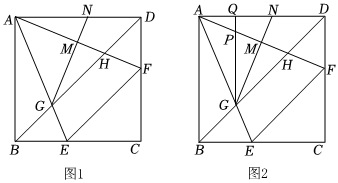
發布：2025/5/22 15:30:1組卷：286引用：1難度：0.1 -
3．在Rt△ABC中，∠BAC=90°，點P在線段BC上，∠BPD=
∠ACB，PD交BA于點D，過點B作BE⊥PD，垂足為E，交CA的延長線于點F．12
（1）如果∠ACB=45°，
①如圖1，當點P與點C重合時，求證：BE=PD；12
②如圖2，當點P在線段BC上，且不與點B、點C重合時，問：①中的“BE=PD”仍成立嗎？請說明你的理由；12
（2）如果∠ACB≠45°，如圖3，已知AB=n?AC（n為常數），當點P在線段BC上，且不與點B、點C重合時，請探究的值（用含n的式子表示），并寫出你的探究過程．BEPD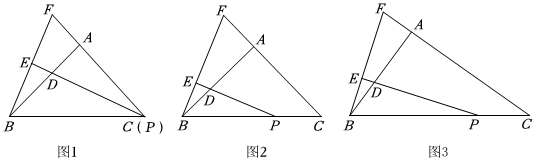
發布：2025/5/22 15:30:1組卷：475引用：1難度：0.1