【問題提出】在由m×n（m×n＞1）個小正方形（邊長為1）組成的矩形網格中，該矩形的一條對角線所穿過的小正方形個數與m,n有何關系？
【問題探究】
為探究規律，我們采用一般問題特殊化的策略，通過分類討論，先從最簡單的情形入手，再逐次遞進，從中找出解決問題的方法．
探究一：
當m,n互質（m,n除1外無其他公因數）時，觀察圖1并完成下表：
| 矩形橫長m | 2 | 3 | 3 | 5 | 4 | 5 | … |
| 矩形縱長n | 1 | 1 | 2 | 2 | 3 | 3 | … |
| 矩形一條對角線所穿過的小正方形個數f | 2 | 3 | 4 | 6 | 6 | x | … |
7
7
．結論：當m,n互質時，在m×n的矩形網格中，該矩形一條對角線所穿過的小正方形的個數f與m,n之間的關系式是
f=m+n-1
f=m+n-1
．探究二：當m,n不互質時，不妨設m=ka,n=kb（a,b,k為正整數，且a,b互質），觀察圖2并完成下表：
| a | 2 | 3 | 3 | 5 | 2 | 3 | … |
| b | 1 | 1 | 2 | 2 | 1 | 1 | … |
| k | 2 | 2 | 2 | 2 | 3 | 3 | … |
| 矩形一條對角線所穿過的小正方形個數f | 4 | 6 | 8 | y | 6 | z | … |
12
12
，z=9
9
．結論：當m,n不互質時，若m=ka,n=kb（a,b,k為正整數，且a,b互質）．在m×n的矩形網格中，該矩形一條對角線所穿過的小正方形的個數f與a,b,k之間的關系式是
f=k（a+b-1）
f=k（a+b-1）
．【模型應用】
一個由邊長為1的小正方形組的長為630，寬為490的矩形網格中，該矩形的一條對角線所穿過的小正方形的個數是
1050
1050
個．【模型拓展】
如圖3，在一個由48個棱長為1的小正方體組成的長方體中，經過頂點A，B的直接穿過的小正方體的個數是
6
6
個．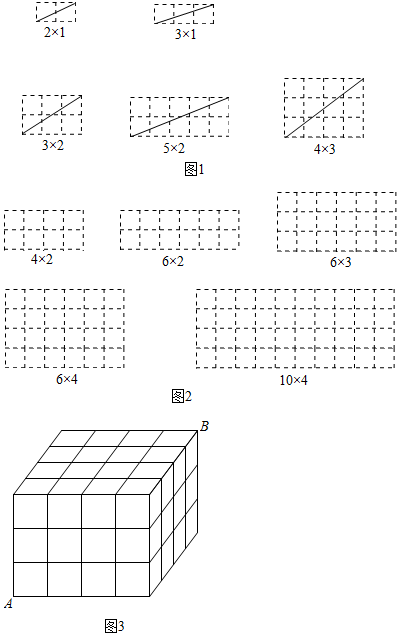
【考點】規律型：圖形的變化類；勾股定理．
【答案】7；f=m+n-1；12；9；f=k（a+b-1）；1050；6
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/25 19:30:2組卷：131引用：1難度：0.7
相似題
-
1．如圖，將一條長度為1的線段三等分，然后取走其中的一份，稱為第一次操作；再將余下的每一條線段三等分，然后取走其中一份，稱為第二次操作；…如此重復操作，當第n次操作結束時，被取走的所有線段長度之和為．
發布：2025/5/25 21:0:1組卷：829引用：45難度：0.7 -
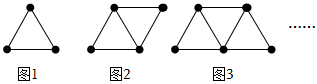
2．如圖是用火柴棍拼成一個由三角形組成的圖形，拼第一個圖形共需要3根火柴棍；拼第二個圖形共需要5根火柴棍；拼第三個圖形共需要7根火柴棍；…照這樣拼圖，則第4個圖形需要 根火柴棍，第n個圖形需要 根火柴棍．
發布：2025/5/26 2:30:2組卷：161引用：4難度：0.7 -
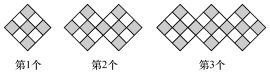
3．如圖是一組有規律的圖案，它們是由邊長相同的小正方形組成，其中部分小正方形涂有陰影，依此規律，第10個圖案中涂有陰影的小正方形的個數為（ ）
發布：2025/5/25 19:30:2組卷：652引用：4難度：0.6