【閱讀材料】
在“相交線與平行線”的學習中,有這樣一道典型問題:
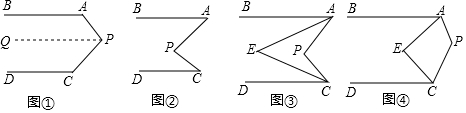
如圖①,AB∥CD,點P在AB與CD之間,可得結論:∠BAP+∠APC+∠PCD=360°.
理由如下:
過點P作PQ∥AB.
∴∠BAP+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD.
∴∠PCD+∠CPQ=180°.
∴∠BAP+∠APC+∠PCD
=∠BAP+∠APQ+∠CPQ+∠PCD
=180°+180°
=360°.
【問題解決】
(1)如圖②,AB∥CD,點P在AB與CD之間,可得∠BAP,∠APC,∠PCD間的等量關系是∠APC=∠A+∠C∠APC=∠A+∠C;(只寫結論)
(2)如圖③,AB∥CD,點P,E在AB與CD之間,AE平分∠BAP,CE平分∠DCP.寫出∠AEC與∠APC間的等量關系,并寫出理由;
(3)如圖④,AB∥CD,點P,E在AB與CD之間,∠BAE=13∠BAP,∠DCE=13∠DCP,可得∠AEC與∠APC間的等量關系是∠APC+3∠AEC=360°∠APC+3∠AEC=360°(只寫結論)
1
3
1
3
【考點】平行線的判定與性質.
【答案】∠APC=∠A+∠C;∠APC+3∠AEC=360°
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:631引用:3難度:0.4
相似題
-
 1.如圖,下列推理正確的是( )
1.如圖,下列推理正確的是( )A.∵∠A=∠D(已知),∴AB∥DE(同位角相等,兩直線平行) B.∵∠B=∠DEF(已知),∴AB∥DE(兩直線平行,同位角相等) C.∵∠A+∠AOE=180°(已知),∴AC∥DF(同旁內角互補,兩直線平行) D.∵AC∥DF(已知),∴∠F+∠ACF=180°(兩直線平行,同旁內角互補) 發布:2025/6/25 8:30:1組卷:197引用:10難度:0.7 -
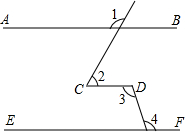 2.如圖,∠1=120°,∠2=60°,∠3=100°,則∠4=時,AB∥EF.發布:2025/7/1 13:0:6組卷:1881引用:27難度:0.9
2.如圖,∠1=120°,∠2=60°,∠3=100°,則∠4=時,AB∥EF.發布:2025/7/1 13:0:6組卷:1881引用:27難度:0.9 -
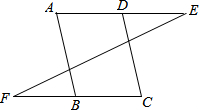 3.如圖,從下列三個條件中:(1)AD∥CB,(2)AB∥CD,(3)∠A=∠C,任選兩個作為條件,另一個作為結論,編一道數學題,并說明理由.
3.如圖,從下列三個條件中:(1)AD∥CB,(2)AB∥CD,(3)∠A=∠C,任選兩個作為條件,另一個作為結論,編一道數學題,并說明理由.
已知:;結論:;理由:.發布:2025/7/1 13:0:6組卷:73引用:4難度:0.5


