定義：對于關于x的一次函數y=kx+b（k≠0），我們稱函數y=kx+b,（x≤a） -kx-b,（x＞a）
為一次函數y=kx+b（k≠0）的“a變換函數”（其中a為常數）．
例如：對于關于x的一次函數y=2x+1的“5變換函數”為2x+1，（x≤5） -2x-1，（x＞5）
．
（1）一次函數y=-x+1的“0變換函數”為y=-x+1，（x≤0） x-1，（x＞0）
-x+1，（x≤0） x-1，（x＞0）
．
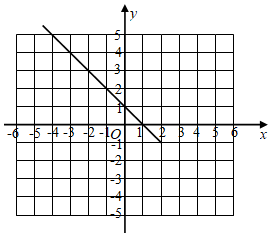
（2）在網格中補全一次函數y=-x+1的“2變換函數”圖象，并完成下列問題：
①對于一次函數y=-x+1的“2變換函數”，當x=3時，求y的值；當y=2時，求x的值；
②對于一次函數y=-x+1的“2變換函數”，當-3≤x≤3時，y的取值范圍是 -1≤y≤4-1≤y≤4．
（3）當一次函數y=-x+1的“a變換函數”與直線y=2有一個交點時，直接寫出a的取值范圍．
kx + b , （ x ≤ a ） |
- kx - b , （ x ＞ a ） |
2 x + 1 ， （ x ≤ 5 ） |
- 2 x - 1 ， （ x ＞ 5 ） |
- x + 1 ， （ x ≤ 0 ） |
x - 1 ， （ x ＞ 0 ） |
- x + 1 ， （ x ≤ 0 ） |
x - 1 ， （ x ＞ 0 ） |
【考點】一次函數圖象上點的坐標特征；一次函數的性質．
【答案】
；-1≤y≤4
- x + 1 ， （ x ≤ 0 ） |
x - 1 ， （ x ＞ 0 ） |
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 21:30:1組卷：729引用：2難度：0.4