生活中，把長與寬之比為2的矩形紙片稱為標準紙（即A4紙）．請思考解決下列問題：
（1）一張標準紙的長為10，則標準紙的寬為：5252；
（2）已知三角形紙片△ABC，AB=AC=6，BC=4．點E、F分別為AB、AC邊的中點，把它沿EF剪開后，再將三角形紙片△AEF沿高線AD剪開，分成①②兩個三角形，拼成如圖1所示的矩形BCMN．矩形紙片BCMN是“標準紙”嗎？如果是，請證明結論；如果不是，請說明理由；
（3）如圖2，在標準紙片ABCD中，長邊AD=8，取邊AD的中點E，將△ABE沿著BE邊折疊得到△BEF，延長BF交邊DC于點H，點M為CH的中點，點N是邊BC上一點，將△MCN沿著MN折疊得到△MNG，當點G落在線段BH上時，求出tan∠CNM的值．
2
2
2
【考點】四邊形綜合題．
【答案】5
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/7 8:0:9組卷：235引用：1難度：0.1
相似題
-
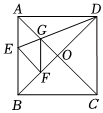1．如圖，正方形ABCD中，對角線AC、BD交于點O，折疊正方形紙片ABCD，使AD落在BD上，點A恰好與BD上的點F重合，展開后折痕DE分別交AB、AC于點E、G，連結GF，給出下列結論：①∠AGD=110.5°；②2tan∠AED=2；③S△AGD=S△OGD；④四邊形AEFG是菱形；⑤BF=OF；⑥若S△OGF=1，則正方形ABCD的面積是12+82．其中正確的個數是（ ）2發布：2025/5/22 20:30:1組卷：52引用：1難度：0.2 -
2．四邊形ABCD是正方形，E是直線BC上一點，連接AE，在AE右側，過點E作射線EP⊥AE，F為EP上一點．
（1）如圖1，若點E是BC邊的中點，且EF=AE，連接CF，則∠DCF=°；
（2）如圖2，若點E是BC邊上一點（不與B，C重合）．∠DCF=45°，判斷線段EF與AE的數量關系，并說明理由；
（3）若正方形邊長為1，且EF=AE，當AF+BF取最小值時，求△BCF的面積．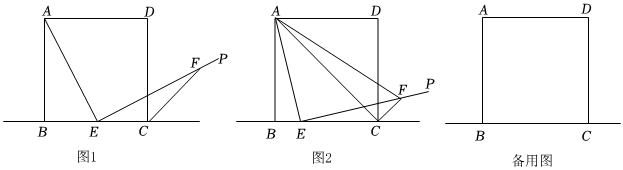
發布：2025/5/22 20:30:1組卷：147引用：4難度：0.3 -
3．如圖，在矩形ABCD中，AB=6cm,BC=2cm.點P從點A出發，沿射線AB方向運動，在運動過程中，以線段AP為斜邊作等腰直角三角形APQ．當PQ經過點C時，點P停止運動．設點P的運動距離為x（cm），△APQ與矩形ABCD重合部分的面積為y（cm2）．
（1）當點Q落在CD邊上時，x=cm；
（2）求y與x之間的函數關系式，并寫出自變量x的取值范圍；
（3）設PQ的中點為M，直接寫出在整個運動過程中，點M移動的距離．發布：2025/5/22 20:0:1組卷：125引用：2難度：0.2