菱形ABCD的邊長為30，∠ADC=120°，點O是對角線AC中點，M是線段OC上任一點，連接DM，作∠DMN=120°，邊MN與直線AB相交于點N．
小南和小浦觀察以上問題時，猜想DM=MN，老師引導他們用“從特殊到一般”的思想方法去嘗試研究．
【特例發現】
小南發現：當點M與點 CC重合時，DM與MN的長度相等，為 3030；
【探究證明】
小浦認為當N在線段AB上時，均有“DM=MN”，請幫助完成證明．
【拓展運用】
①連結DN交AC于點E，求證：∠ADE+∠MDC為定值．
②當MN2+DE2=AE2時，S△ADE=2253-2252253-225．
3
3
【考點】四邊形綜合題．
【答案】C；30；225-225
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：55引用：1難度：0.2
相似題
-
1．如圖，在菱形ABCD中，M，N分別是邊AB，BC的中點，MP⊥AB交邊CD于點P，連接NM，NP．
（1）若∠B=60°，這時點P與點C重合，則∠NMP=度；
（2）求證：NM=NP；
（3）當△NPC為等腰三角形時，求∠B的度數．
發布：2025/6/19 1:30:1組卷：2881引用：6難度：0.5 -
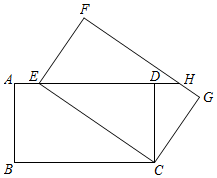2．如圖，將矩形ABCD繞點C旋轉得到矩形FECG，點E在AD上，延長ED交FG于點H．
（1）求證：△EDC≌△HFE；
（2）連接BE、CH．
①四邊形BEHC是怎樣的特殊四邊形？證明你的結論；
②若BC長為，則AB的長為 時，四邊形BEHC為菱形．3發布：2025/6/19 21:0:2組卷：117引用：1難度：0.4 -
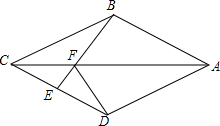3．如圖，在四邊形ABCD中，AB=AD，CB=CD，E是CD上一點，BE交AC于F，連接DF．
（1）證明：∠BAC=∠DAC，∠AFD=∠CFE；
（2）若AB∥CD，試證明四邊形ABCD是菱形；
（3）在（2）的條件下，若BE⊥CD，試證明∠EFD=∠BCD．發布：2025/6/18 8:30:2組卷：215引用：3難度：0.1