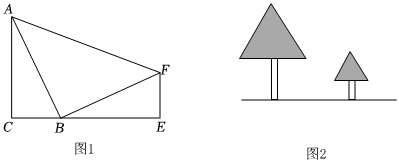
如圖1，點B在線段CE上，AC⊥CE，FE⊥CE，垂足分別為C、E，且AC=BE，BC=EF，連接AB、BF、AF，解答下列問題：
（1）判斷△ABF的形狀，并說明理由；
（2）梯形是只有一組對邊平行的四邊形，平行的兩邊叫做梯形的底邊，較短的一條底邊叫上底，較長的一條底邊叫下底，另外兩邊叫腰，夾在兩底之間的垂線段叫梯形的高．梯形的面積公式為：12×（上底+下底）×高．
若AB=c,AC=b,BC=a,且四邊形ACEF為梯形．請通過求梯形ACEF面積不同的計算方法驗證：在Rt△ABC中，兩直角邊a、b和斜邊c滿足a2+b2=c2；
（3）利用（2）中驗證的結論解答下列問題：
①若Rt△ABC兩條直角邊長分別為3、4，則斜邊的長為 55；
②如圖2，有兩棵樹，一棵高12米，另一棵高5米，兩棵樹樹梢相距8米，一只鳥從矮樹的樹梢飛到另一棵數的最短距離是 113113米．
1
2
113
113
【考點】三角形綜合題．
【答案】5；
113
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：26引用：1難度：0.2
相似題
-
1．已知點A（0，y）在y軸正半軸上，以OA為邊作等邊△OAB，其中y是方程
的解．32y-2+12=3y-1
（1）求點A的坐標；
（2）如圖1，點P在x軸正半軸上，以AP為邊在第一象限內作等邊△APQ，連QB并延長交x軸于點C，求證OC=BC；
（3）如圖2，若點M為y軸正半軸上一動點，點M在點A的上邊，連MB，以MB為邊在第一象限內作等邊△MBN，連NA并延長交x軸于點D，當點M運動時，DN-AM的值是否發生變化？若不變，求出其值；若變化，求出其變化的范圍．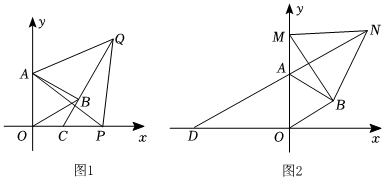
發布：2025/6/3 6:0:2組卷：444引用：5難度：0.2 -
2．閱讀理解，自主探究：
“一線三垂直”模型是“一線三等角”模型的特殊情況，即三個等角角度為90°，于是有三組邊相互垂直．所以稱為“一線三垂直模型”．當模型中有一組對應邊長相等時，則模型中必定存在全等三角形．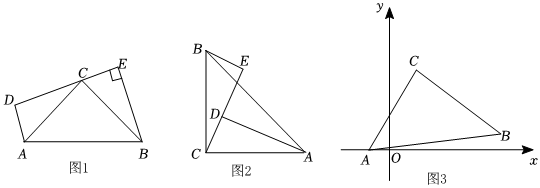
（1）問題解決：如圖1，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點C作直線DE，AD⊥DE于D，BE⊥DE于E，則CD與BE的數量關系是 ；
（2）問題探究：如圖2，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點C作直線CE，AD⊥CE于D，BE⊥CE于E，AD=2.5cm,DE=1.6cm,求BE的長；
（3）拓展延伸：如圖3，在平面直角坐標系中，A（-1.5，0），C（1.5，3.5），△ABC為等腰直角三角形，∠ACB=90°，AC=BC，求B點坐標．發布：2025/6/3 6:0:2組卷：1023引用：4難度：0.1 -
3．關于等邊三角形，有很多值得我們探究的，在一次數學課上，老師出示了如下框中的題目．
第一小組討論后，進行了如下解答：已知：如圖，在等邊△ABC中，點D在AC上，點E在BC的延長線，且BD=ED．試判斷AD與CE的數量關系，并說明理由．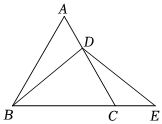 
（1）特殊情況，探索結論
當點D為AC的中點時，如圖1，線段AD CE．（填“＞”，“＜”或“=”）
（2）特例啟發，解答題目
當點D不是AC的中點時，線段AD CE．（填“＞”，“＜”或“=”）
理由如下：
如圖2，過點D作DF∥BC，交AB于點F．（請你完成后面的解答過程）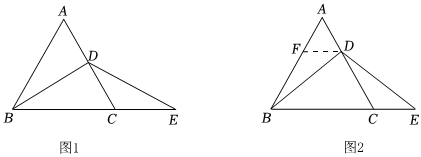
發布：2025/6/3 7:30:2組卷：13引用：1難度：0.3