問題提出：（1）同學們在探索求代數式x2+9+（15-x）2+25的最小值的過程時，老師進行了如下的引導，如圖1，C為線段BD上的一個動點，分別過點B，D作AB⊥BD，ED⊥BD，連接AC，EC．已知AB=4，DE=1，BD=12，設CD=x.
①則AC+CE的長為 x2-24x+160+x2+1x2-24x+160+x2+1．（用含x的代數式表示）
②如圖2，過A作AF⊥DE交ED的延長線于F，構造長方形ABDF，連接AE，此時A、C、E三點共線，AC+CE的值最小，求最小值．
問題解決：（2）請用上述的構圖法求出代數式x2+9+（15-x）2+25的最小值．
x
2
+
9
（
15
-
x
）
2
+
25
x
2
-
24
x
+
160
+
x
2
+
1
x
2
-
24
x
+
160
+
x
2
+
1
x
2
+
9
（
15
-
x
）
2
+
25
【考點】軸對稱-最短路線問題；矩形的性質．
【答案】
x
2
-
24
x
+
160
+
x
2
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/31 0:0:8組卷：435引用：4難度：0.5
相似題
-
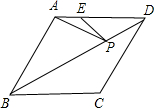1．如圖，在菱形ABCD中，AB=6，∠ABC=60°，點E在AD上，且AE=2，點P是對角線BD上的一個動點，則PE+PA的最小值是．發布：2025/6/8 11:30:1組卷：299引用：2難度：0.7 -
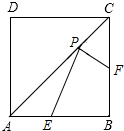2．如圖，正方形ABCD的面積是2，E，F，P分別是AB，BC，AC上的動點，PE+PF的最小值等于．發布：2025/6/8 12:30:1組卷：868引用：16難度：0.5 -
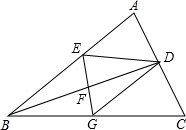3．如圖，BD是△ABC的角平分線，它的垂直平分線分別交AB，BD，BC于點E，F，G，連接ED，DG．
（1）請判斷四邊形EBGD的形狀，并說明理由；
（2）若∠ABC=30°，∠C=45°，ED=2，點H是BD上的一個動點，求HG+HC的最小值．10發布：2025/6/8 13:0:1組卷：397引用：5難度：0.6