某水產養殖戶，一次性收購了20000kg小龍蝦，計劃養殖一段時間后再出售，已知每天放養的費用相同，放養10天的總成本為30.4萬元；放養20天的總成本為30.8萬元（總成本=放養總費用+收購成本）．
（1）設每天的放養費用是a萬元，收購成本為b萬元，求a和b的值；
（2）設這批小龍蝦放養t天后的質量為m（kg），銷售單價y元/kg.根據以往經驗可知：m與t的函數關系式為m=20000（0≤t≤50） 100t+15000（50＜t≤100）
，y與t的函數關系如圖所示．
①求y與t的函數關系式；
②設將這批小龍蝦放養t天后一次性出售所得利潤為W元，求當t為何值時，W最大？并求出W的最大值．（利潤=銷售總額-總成本）
20000 （ 0 ≤ t ≤ 50 ） |
100 t + 15000 （ 50 ＜ t ≤ 100 ） |
【考點】二次函數的應用．
【答案】（1）a的值為0.04，b的值為30；
（2）①y=
；
②t=55時，W最大，最大值為180250元．
（2）①y=
1 5 t + 15 （ 0 ≤ t ≤ 50 ） |
- 1 10 t + 30 （ 50 ＜ t ≤ 100 ） |
②t=55時，W最大，最大值為180250元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：234引用：1難度：0.6
相似題
-
1．某商店試銷一種新商品，新商品的進價為30元/件，經過一段時間的試銷發現，每月的銷售量會因售價的調整而不同．令每月銷售量為y件，售價為x元/件，每月的總利潤為Q元．
（1）當售價在40≤x≤50元時，每月銷售量都為60件，則此時每月的總利潤最多是多少元？
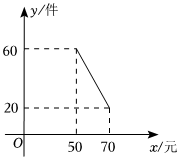
（2）當售價在50≤x≤70元時，每月銷售量與售價的關系如圖所示，則此時當該商品售價x是多少元時，該商店每月獲利最大，最大利潤是多少元？發布：2025/6/8 9:0:1組卷：56引用：3難度：0.6 -
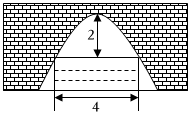2．如圖所示為一座縱截面為拋物線形狀的拱橋，當水面寬4m時，拱頂（拱橋洞的最高點）離水面2m,當水位下降1m時，水面的寬度為（ ）發布：2025/6/8 9:0:1組卷：105引用：1難度：0.6 -
3．為了鞏固脫貧攻堅成效，助推鄉村振興，最近市委市政府又出臺了系列“惠農”政策，農民收入大幅增加．某村一農戶生產經銷一種農副產品，已知這種產品的成本為5元/千克，售價為6元/千克時，當天的銷售量為100千克．在銷售過程中發現：售價每上漲0.5元，當天的銷售量就減少5千克．設當天銷售單價統一為x元/千克（x≥6，且x是按0.5元的整數倍上漲），當天的銷售利潤為y元．
（1）求y與x之間的函數關系式，不要求寫出自變量x的取值范圍；
（2）若物價部門核定該產品的利潤率不得超過80%，該產品的售價定為多少元時，才能使當天獲得最大利潤？最大利潤是多少？發布：2025/6/8 8:0:6組卷：38引用：1難度：0.6