勾股定理是人類早期發現并證明的重要數學定理之一,是用代數思想解決問題的最重要工具之一,也是數形結合的紐帶之一.它不但因證明方法層出不窮吸引著人們,更因為應用廣泛而使人入迷.
(1)證明勾股定理
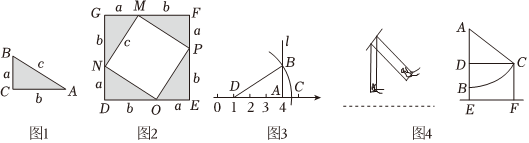
取4個與Rt△ABC(圖1)全等的三角形,其中∠=90°,AB=c,BC=a,AC=b,把它們拼成邊長為a+b的正方形DEFG,其中四邊形OPMN是邊長為c的正方形,如圖2,請你利用以下圖形驗證勾股定理.
(2)應用勾股定理
①應用場景1:在數軸上畫出表示無理數的點.如圖3,在數軸上找出表示1的點D和表示4的點A,過點A作直線l垂直于DA,在l上取點B,使AB=2,以點D為圓心,DB為半徑作弧,則弧與數軸的交點C表示的數是 13+113+1;
②應用場景2:解決實際問題.如圖4,某公園有一秋千,秋千靜止時,踏板離地的垂直高度BE=0.5m,將它往前推至C處時,水平距離CD=2m,踏板離地的垂直高度CF=1.5m,它的繩索始終拉直,求繩索AC的長.
13
+
1
13
+
1
【答案】
13
+
1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/30 8:0:9組卷:125引用:2難度:0.6
相似題
-
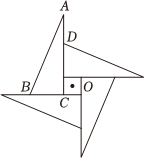 1.10.《時代數學學習》雜志2007年3月將改版為《時代學習報?數學周刊》,其徽標是我國古代“弦圖”的變形(見示意圖).該圖可由直角三角形ABC繞點O同向連續旋轉三次(每次旋轉90°)而得.因此有“數學風車”的動感.假設中間小正方形的面積為1,整個徽標(含中間小正方形)的面積為92,AD=2,則徽標的外圍周長為( )
1.10.《時代數學學習》雜志2007年3月將改版為《時代學習報?數學周刊》,其徽標是我國古代“弦圖”的變形(見示意圖).該圖可由直角三角形ABC繞點O同向連續旋轉三次(每次旋轉90°)而得.因此有“數學風車”的動感.假設中間小正方形的面積為1,整個徽標(含中間小正方形)的面積為92,AD=2,則徽標的外圍周長為( )A.40 B.44 C.46 D.48 發布:2025/1/25 8:0:2組卷:366引用:2難度:0.6 -
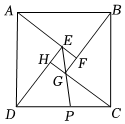 2.如圖是中國古代數學家趙爽用來證明勾股定理的弦圖示意圖,它是由四個全等的直角三角形和一個小正方形EFGH組成,恰好拼成一個大正方形ABCD,連結EG并延長交CD于點P.若AE=3EF=3,則DP的長為( )
2.如圖是中國古代數學家趙爽用來證明勾股定理的弦圖示意圖,它是由四個全等的直角三角形和一個小正方形EFGH組成,恰好拼成一個大正方形ABCD,連結EG并延長交CD于點P.若AE=3EF=3,則DP的長為( )A. 207B. 209C.3 D. 157發布:2025/5/22 3:30:2組卷:582引用:4難度:0.4 -
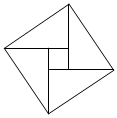 3.?我國古代數學家趙爽巧妙地用“弦圖”證明了勾股定理,標志著中國古代的數學成就.如圖,若弦圖中四個全等的直角三角形的兩條直角邊長分別為3和4,則中間小正方形的對角線長為 .發布:2025/5/23 3:30:1組卷:151引用:1難度:0.8
3.?我國古代數學家趙爽巧妙地用“弦圖”證明了勾股定理,標志著中國古代的數學成就.如圖,若弦圖中四個全等的直角三角形的兩條直角邊長分別為3和4,則中間小正方形的對角線長為 .發布:2025/5/23 3:30:1組卷:151引用:1難度:0.8


