問題情境:
數學活動課上,同學們開展了以“矩形紙片折疊”為主題的探究活動,已知矩形紙片邊長分別為AB=a,AD=b(a<b).
動手實踐:
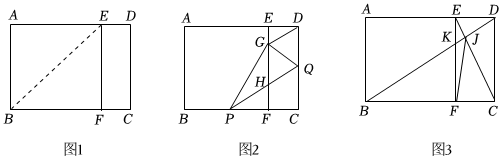
如圖1,小華將矩形紙片ABCD折疊,點A落在BC邊上的點F處,折痕為BE,連接EF,然后將紙片展平,得到正方形AEFB,矩形CDEF.
(1)折痕BE的長為 2a2a;(用含a的式子表示)
(2)如圖2,若P為線段BF上的任意一點,Q為CD的中點,小芳繼續將矩形紙片ABCD沿經過P,Q兩點的直線折疊,使點C落在折痕EF上的點G,折痕PQ與折痕EF交于點H,小芳同學不斷改變點P的位置,發現四邊形DGHQ是某種特殊四邊形.
①請你判斷四邊形DGHQ的形狀,并給予證明:
②若∠PPC=30°,求四邊形DGHQ的周長.(用含a的式子表示)
深度探究:
(3)小強在圖1中連接BD和CE交于點J,BD與折痕EF交于點K,連接FJ,如圖3,當BD⊥CE時,BJ-EJFJ是否為定值?若是,請求出定值;若不是,請說明理由.
 ?
?
2
2
BJ
-
EJ
FJ
【考點】四邊形綜合題.
【答案】a
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/8 8:0:9組卷:194引用:1難度:0.3
相似題
-
1.在人教版八年級上冊數學教材P53的數學活動中有這樣一段描述:在四邊形ABCD中,AD=CD,AB=CB,我們把這種兩組鄰邊分別相等的四邊形叫做“箏形”,如圖(1).
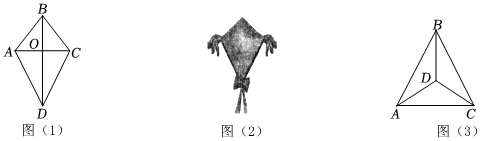
(1)知識應用:小風想要做一個如圖(2)所示的風箏,他想先固定中間的“十字架”,再確定四周,從數學的角度看,小風確定“十字架”時應滿足什么要求?并證明你的結論.
(2)知識拓展:如圖(3)所示,如果D為△ABC內一點,BD平分∠ABC,且AD=CD,試證明:AB=CB.發布:2025/6/9 0:30:2組卷:72引用:1難度:0.2 -
2.(1)如圖1,在四邊形ABCD中,∠B=∠C=90°,點E是邊BC上一點,AB=EC,BE=CD,連接AE、DE.判斷△AED的形狀,并說明理由;
(2)在平面直角坐標系中,已知點A(2,0),點B(5,1),點C在第一象限內,若△ABC是等腰直角三角形,求點C的坐標;
(3)如圖2,在平面直角坐標系中,已知點A(0,1),點C是x軸上的動點,線段CA繞著點C按順時針方向旋轉90°至線段CB,連接BO、BA,則BO+BA的最小值是 . 發布:2025/6/8 23:30:1組卷:886引用:3難度:0.3
發布:2025/6/8 23:30:1組卷:886引用:3難度:0.3 -
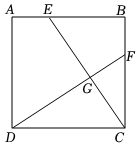 3.如圖,正方形ABCD中,AE=BF.
3.如圖,正方形ABCD中,AE=BF.
(1)求證:△BCE≌△CDF;
(2)求證:CE⊥DF;
(3)若CD=6,且DG2+GE2=41,則BE=.發布:2025/6/8 23:30:1組卷:360引用:3難度:0.6


