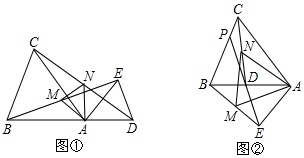
已知：如圖①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=α，且點B，A，D在一條直線上，連接BE，CD，M，N分別為BE，CD的中點．
（1）求證：①BE=CD；
②△AMN是等腰三角形；
（2）在圖①的基礎(chǔ)上，將△ADE繞點A按逆時針方向旋轉(zhuǎn)180°，其他條件不變，得到圖②所示的圖形．請直接寫出（1）中的兩個結(jié)論是否仍然成立．
【考點】相似形綜合題．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/13 10:0:8組卷：1222引用：5難度：0.1
相似題
-
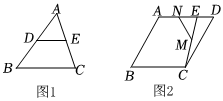1．課本再現(xiàn)：
如圖1，DE是△ABC的中位線．求證：DE∥BC，DE=BC．12
小明思考了一會，覺得可以通過證△ADE∽△ABC從而得到該定理的證明．
定理證明：
（1）請你根據(jù)小明的思路，結(jié)合圖1，給出該定理的證明過程．
定理運用：
（2）如圖2，在菱形ABCD中，∠B=60°，E是AD上一點，M，N分別是CE，AE的中點，且MN=1，則菱形ABCD的周長為 ．發(fā)布：2025/6/6 16:0:1組卷：50引用：1難度：0.6 -
2．【基礎(chǔ)鞏固】
（1）如圖1，在△ABC中，AB=AC，CD⊥AB，求證：∠A=2∠BCD．
【嘗試應(yīng)用】
（2）如圖2，在△ABC中，∠B=90°，D為邊AB上一點，∠A=2∠BCD，BD?AC=5．求CD的長．
【嘗試應(yīng)用】
（3）如圖3，四邊形ABCD為矩形，連接BD，將矩形ABCD繞點B旋轉(zhuǎn)至矩形EBFG，使得邊EG經(jīng)過點C，EG交BD于點H，若EH=CG=1，求BH2的值．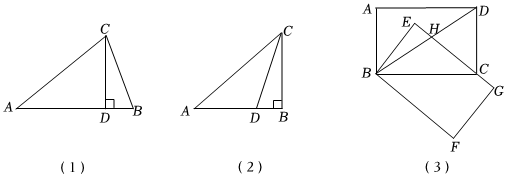
發(fā)布：2025/6/6 8:30:1組卷：318引用：2難度：0.2 -
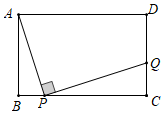3．如圖，在矩形ABCD中，點P是BC邊上任意一點（點P不與B、C重合），連接AP，作PQ⊥AP，交CD于點Q，若AB=3，BC=4．
（1）試證明：△ABP∽△PCQ；
（2）當(dāng)BP為多少時，CQ最長，最長是多少？
（3）試探究，是否存在一點P，使△APQ是等腰直角三角形？發(fā)布：2025/6/6 4:0:1組卷：209引用：4難度：0.2
相關(guān)試卷