如圖①，平面四邊形ABDE由直角梯形ACDE和Rt△ACB組成，AC⊥BD，BC=CD=DE=1，AC=3，DE∥AC．如圖②，沿著直線AC將直角梯形ACDE折起至點D和點M重合，點E和點N重合，使得二面角M-AC-B的大小為60°．
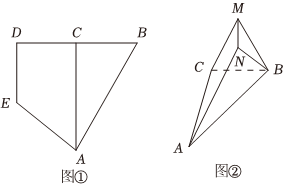
（1）求點A到直線BM的距離；
（2）若點P是線段AC上的動點，是否存在點P，使得平面BMN與平面BPN的夾角的余弦值為105？若存在，求出CP的長度；若不存在，請說明理由．
3
10
5
【考點】二面角的平面角及求法；點、線、面間的距離計算．
【答案】（1）．
（2）存在點P，使得平面BMN與平面BPN的夾角的余弦值為，此時CP=．
15
2
（2）存在點P，使得平面BMN與平面BPN的夾角的余弦值為
10
5
3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：77引用：2難度：0.5
相似題
-
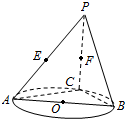1．如圖，AB是圓O的直徑，點C是圓O上異于A，B的點，直線PC⊥平面ABC，E，F分別是PA，PC的中點．
（Ⅰ）記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系，并加以證明；
（Ⅱ）設（Ⅰ）中的直線l與圓O的另一個交點為D，且點Q滿足．記直線PQ與平面ABC所成的角為θ，異面直線PQ與EF所成的角為α，二面角E-l-C的大小為β．求證：sinθ=sinαsinβ．DQ=12CP發布：2025/1/20 8:0:1組卷：927引用：12難度：0.1 -
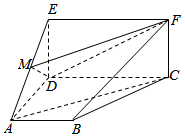2．如圖，四邊形ABCD為梯形，四邊形CDEF為矩形，平面ABCD⊥平面CDEF，∠BAD=∠ADC=90°，AB=AD=DE=CD，M為AE的中點．12
（1）證明：AC∥平面MDF；
（2）求平面MDF與平面BCF的夾角的大小．發布：2025/1/2 8:0:1組卷：141引用：1難度：0.6 -
3．如圖，AB是圓O的直徑，PA垂直于圓所在的平面，C是圓周上的點．
（1）求證：平面PAC⊥平面PBC；
（2）若AB=2，AC=2，PA=2，求二面角C-PB-A的度數．2發布：2025/1/28 8:0:2組卷：33引用：1難度：0.5