如圖，在Rt△ABC中，∠ACB=90°，D為AB邊上的一點，以AD為直徑的⊙O交BC于點E，交AC于點F，過點C作CG⊥AB交AB于點G，交AE于點H，過點E的弦EP交AB于點Q（EP不是直徑），點Q為弦EP的中點，連接BP，BP恰好為⊙O的切線．
（1）求證：BC是⊙O的切線．
（2）求證：?EF=?ED．
（3）若sin∠ABC=35，AC=15，求四邊形CHQE的面積．
?
EF
?
ED
3
5
【考點】圓的綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1787引用：3難度：0.2
相似題
-
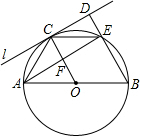1．如圖，AB為⊙O的直徑，C為半圓上一動點，過點C作⊙O的切線l,過點B作BD⊥l,垂足為D，BD與⊙O交于點E，連接OC，CE，AE，AE交OC于點F．
（1）求證：△CDE≌△EFC；
（2）若AB=4，連接AC．
①當AC=時，四邊形OBEC為菱形；
②當AC=時，四邊形EDCF為正方形．發布：2025/5/23 23:30:1組卷：963引用：8難度：0.5 -
2．如圖①，已知⊙O是△ABC的外接圓，∠ABC=∠ACB=α（45°＜α＜90°，D為
上一點，連接CD交AB于點E．?AB
（1）連接BD，若∠CDB=40°，求α的大小；
（2）如圖②，若點B恰好是中點，求證：CE2=BE?BA；?CD
（3）如圖③，將CD分別沿BC、AC翻折得到CM、CN，連接MN，若CD為直徑，請問是否為定值，如果是，請求出這個值，如果不是，請說明理由．ABMN
發布：2025/5/23 23:30:1組卷：1566引用：4難度：0.3 -
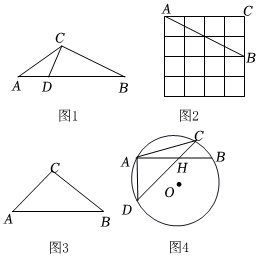3．【閱讀理解】三角形一邊上的點將該邊分為兩條線段，且這兩條線段的積等于這個點到這邊所對頂點連線的平方，則稱這個點為三角形該邊的“好點”．
如圖1，△ABC中，點D是AB邊上一點，連接CD，若CD2=AD?BD，則稱點D是△ABC中AB邊上的“好點”．
【探究應用】
（1）如圖2，△ABC的頂點是4×4網格圖的格點，請僅用直尺畫出（或在圖中直接描出）AB邊上的“好點”；
（2）如圖3，△ABC中，AB=14，cosA=，tanB=22，若點D是AB邊上的“好點”，求線段AD的長；34
（3）如圖4，△ABC是⊙O的內接三角形，點H在AB上，連接CH并延長交⊙O于點D，若點H是△ACD中CD邊上的“好點”．
①求證：AH=BH；
②若BC⊥CH，⊙O的半徑為r,且r=AD，求32的值．DHCH發布：2025/5/23 23:0:1組卷：1365引用：5難度：0.2