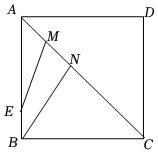
如圖，正方形ABCD的邊長為8，點E在AB上，BE=2，點M，N為AC上動點，且MN=2
2
，連接BN，EM，則四邊形BEMN周長的最小值為
12+2
2
12+2
2
．

【答案】12+2

【解答】

【點評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/6/10 10:0:2組卷：736引用：5難度：0.3

相似題

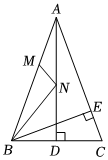1．如圖，△ABC中，AB=AC=2，∠ACB=75°，AD，BE為高．點M，N分別為AB，AD上的動點，那么MN+BN的最小值為
．
發(fā)布：2025/6/10 8:30:1組卷：173引用：3難度：0.5
解析
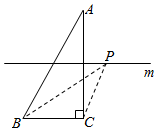2．如圖，在△ABC中，∠C=90°，∠A=30°，BC=1，直線m垂直平分AC，點P為直線m上的動點，則PB+PC的最小值是
．
發(fā)布：2025/6/10 13:0:2組卷：87引用：6難度：0.7
解析
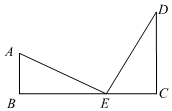3．11世紀(jì)的一位阿拉伯?dāng)?shù)學(xué)家曾提出一個“鳥兒捉魚”問題：小溪邊長著兩棵棕櫚樹，恰好隔岸相望，一棵棕櫚樹CD高是6米，另外一棵AB點高4米；AB與CD樹干間的距離是10米．每棵樹的樹頂上都停著一只鳥，忽然，兩只鳥同時看見棕櫚樹間的水面上游出一條魚，它們立刻以相同的速度飛去抓魚，并且同時到達(dá)目標(biāo)E．
（1）問：這條魚出現(xiàn)的地方離比較高的棕櫚樹的樹根C有多遠(yuǎn)？
（2）求
16
+
x
2
+
36
+
（
10
-
x
）
2
的最小值
．
發(fā)布：2025/6/10 11:0:1組卷：147引用：4難度：0.5
解析

相關(guān)試卷

如圖，正方形ABCD的邊長為8，點E在AB上，BE=2，點M，N為AC上動點，且MN=22，連接BN，EM，則四邊形BEMN周長的最小值為 12+2212+22．