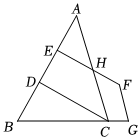
如圖，CD⊥AB于D，FE⊥AB于E．∠ACD+∠F=180°．將證明AC∥FG的過程補充完整．
證明：∵CD⊥AB，FE⊥AB，（已知）
∴∠AEF=∠ADC=90°，
∴EF∥DC，（ 同位角相等，兩直線平行同位角相等，兩直線平行）
∴∠AHE=∠ACD，（ 兩直線平行，同位角相等兩直線平行，同位角相等）
∵∠ACD+∠F=180°，
∴∠AHE+∠F=180°，（ 等量代換等量代換）
∵∠AHE=∠FHC，（對頂角相等）
∴∠FHC+∠F=180°，（等量代換）
∴AC∥FG．（ 同旁內角互補，兩直線平行同旁內角互補，兩直線平行）
【考點】平行線的判定與性質．
【答案】同位角相等，兩直線平行；兩直線平行，同位角相等；等量代換；同旁內角互補，兩直線平行
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 13:0:1組卷：19引用：2難度：0.6
相似題
-
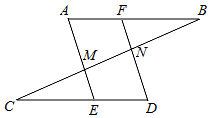1．如圖，AB∥CD，∠A=∠D，有下列結論：①∠B=∠C；②AE∥DF；③AE⊥BC；④∠AMC=∠BND．其中正確的有．（只填序號）發布：2025/6/7 23:30:2組卷：363引用：5難度：0.7 -
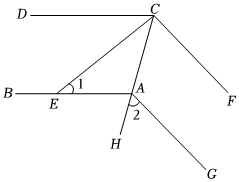2．如圖，AB∥CD，CE平分∠ACD，CF⊥CE，∠1=35°，
（1）求∠ACE的度數；
（2）若∠2=55°，求證：CF∥AG．發布：2025/6/7 23:30:2組卷：105引用：4難度：0.7 -
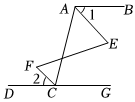3．完成下面的推理過程．已知：如圖，∠BAC與∠GCA互補，∠1=∠2，求證：∠E=∠F．
證明：∵∠BAC與∠GCA互補．
即 ，
∴AB∥DG（ ）．
∴∠BAC=∠ACD．（ ）．
又∵∠1=∠2，（已知）．
∴∠BAC-∠1=∠ACD-∠2，即∠EAC=∠FCA．（ ）．
∴∥（內錯角相等，兩直線平行）．
∴∠E=∠F．（ ）．發布：2025/6/7 23:30:2組卷：90引用：1難度：0.6