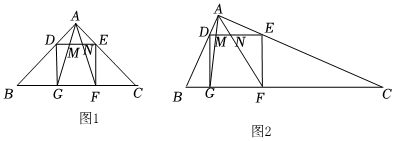
在△ABC中，∠BAC=90°，正方形DEFG的四個頂點在△ABC的邊上，連接AG，AF分別交DE于M，N兩點．
（1）嘗試探究：如圖1，當AB=AC=1時，DE的長為 2323，MN的長為 2929；
（2）類比延伸：如圖2，若AB=1，AC=2，求DE和MN的長．
小明思考后，寫出了如下部分解題過程，請你幫他補充完整：
證明：∵∠BAC=90°，四邊形DEFG為正方形．
∴∠B+∠C=90°，∠CEF+∠C=90°．
∴∠B=∠CEF．
∴∠BGD=∠EFC=∠BAC=90°．
又∵∠ACB=∠FCE．
∴△BGD∽△EFC∽△BAC．
……
（3）拓展遷移：在（2）的條件下，改變AB，AC的長度，當AB＜AC時，直接寫出MN與DM，EN的關系．
2
3
2
3
2
9
2
9
【考點】相似形綜合題．
【答案】；
2
3
2
9
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：57引用：1難度：0.1
相似題
-
1．已知：如圖，正方形ABCD與正方形AEFG．
（1）如圖①，求證：BG=DE；
（2）如圖②，求的值；CFBG
（3）如圖③，分別取CF、BE的中點M、N，試探究：MN與BE的關系，并說明理由．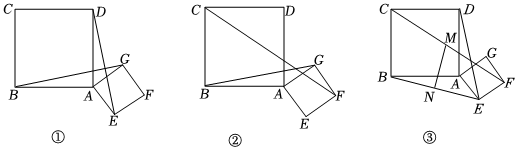
發布：2025/6/9 16:30:1組卷：218引用：3難度：0.2 -
2．【初步探究】
（1）把矩形紙片ABCD如圖①折疊，當點B的對應點B'在MN的中點時，填空：△EB'M △B'AN（“≌”或“∽”）．
【類比探究】
（2）如圖②，當點B的對應點B'為MN上的任意一點時，請判斷（1）中結論是否成立？如果成立，請寫出證明過程；如果不成立，請說明理由．
【問題解決】
（3）在矩形ABCD中，AB=4，BC=6，點E為BC中點，點P為線段AB上一個動點，連接EP，將△BPE沿PE折疊得到△B'PE，連接DE，DB'，當△EB'D為直角三角形時，BP的長為 ．
發布：2025/6/9 14:30:1組卷：832引用：9難度：0.2 -
3．已知AD是△ABC的中線，點E是線段AD上一點，過點E作AC的平行線，過點B作AD的平行線，兩平行線交于點F，連結AF．
【方法感知】如圖①，當點E與點D重合時，易證：△AEC≌△FBE．（不需證明）
【探究應用】如圖②，當點E與點D不重合時，求證：四邊形ACEF是平行四邊形．
【拓展延伸】如圖③，記AB與EF的交點為G，CE的延長線與AB的交點為N，且N為AB的中點．
（1）=；NGGA
（2）若CA⊥AB，BC=5時，則BF的長為 ．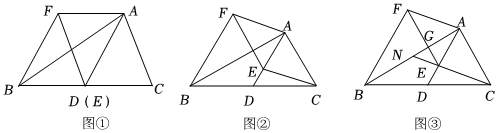
發布：2025/6/9 22:30:2組卷：252引用：5難度：0.3