某課題研究小組就圖形面積問題進行專題研究，他們發現如下結論：
（1）有一條邊對應相等的兩個三角形面積之比等于這條邊上的對應高之比；
（2）有一個角對應相等的兩個三角形面積之比等于夾這個角的兩邊乘積之比；
…
現請你繼續對下面問題進行探究，探究過程可直接應用上述結論．（S表示面積）
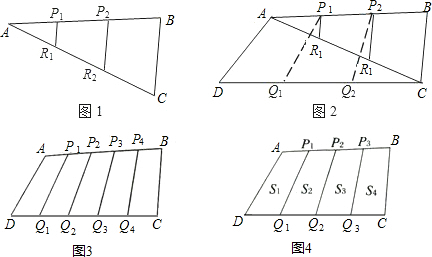
問題1：如圖1，現有一塊三角形紙板ABC，P1，P2三等分邊AB，R1，R2三等分邊AC．經探究知S四邊形P1P2R2R1=13S△ABC，請證明．
問題2：若有另一塊三角形紙板，可將其與問題1中的拼合成四邊形ABCD，如圖2，Q1，Q2三等分邊DC．請探究S四邊形P1Q1Q2P2與S四邊形ABCD之間的數量關系．
問題3：如圖3，P1，P2，P3，P4五等分邊AB，Q1，Q2，Q3，Q4五等分邊DC．若S四邊形ABCD=1，求S四邊形P2Q2Q3P3．
問題4：如圖4，P1，P2，P3四等分邊AB，Q1，Q2，Q3四等分邊DC，P1Q1，P2Q2，P3Q3將四邊形ABCD分成四個部分，面積分別為S1，S2，S3，S4．請直接寫出含有S1，S2，S3，S4的一個等式．
S
四邊形
P
1
P
2
R
2
R
1
1
3
S
四邊形
P
1
Q
1
Q
2
P
2
S
四邊形
P
2
Q
2
Q
3
P
3
【考點】三角形的面積．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：1893引用：8難度：0.5
相似題
-
1．如圖，四邊形OA1A2B1是邊長為1的菱形，∠A1OB1=60°，以對角線OA2為邊作第二個菱形OA2A3B2，∠A2OB2=60°，連接A1A3，得到△A1A2A3；再以對角線OA3為邊作第三個菱形OA3A4B3，∠A3OB3=60°，連接A2A4，得到△A2A3A4；……，則△A2021A2022A2023的面積為 ．
發布：2025/5/24 14:30:1組卷：104引用：1難度：0.6 -
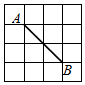2．在網格線中，每個方格的頂點叫做格點，以格點連線為邊的三角形叫做格點三角形，如圖中的網格線中，每個小正方形的邊長均為1，以線段AB為一邊的格點三角形的面積隨著第三個頂點的位置的不同而發生變化，如下列表格中當格點三角形的面積為1時，頻數為8；如果將圖中格點三角形面積記為S，頻數記為x,根據上述信息計算：當S=3時，x=．格點三角形面積（S） 1 2 3 4 頻數（x） 8 發布：2025/5/25 4:30:1組卷：33引用：3難度：0.6 -
3．△ABC三個頂點的坐標分別為A（4，1），B（4，5），C（-1，2），則△ABC的面積為（ ）
發布：2025/5/24 20:0:2組卷：21引用：1難度：0.6