綜合與實踐
問題提出
（1）如圖①，△ABC是等腰三角形，點D，E分別在腰AC，AB上，且BE=CD，連接BD，CE．判斷BD與CE長度的大小關系，并證明；
問題探究
（2）如圖②AD是△ABC的中線，BE交AC于E，交AD于F，若AE=EF，AC=8，則BF=88；
問題解決
（3）今年全國兩會上，不少來自農村、關注“三農”工作的代表委員期待電力在全面推進鄉村振興中發揮越來越重要的作用．某地區規劃出如圖③所示的四邊形ABCD地塊，計劃開發出一個生態宜居，綠色人文的農業觀光區，其中AD⊥CD，BC⊥CD，∠BAD=120°，AE是現有的地下電纜，CE=AB．為滿足農業用電，B點和C點分別設置了風力發電機，現要埋電纜線路BP與線路AC，點P是AE的中點．已知埋每米電纜的費用是a元，請問埋電纜線路AC的費用是線路BP費用的幾倍？并說明理由．
?
【考點】四邊形綜合題．
【答案】8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/7 8:0:9組卷：41引用：1難度：0.3
相似題
-
1．如圖1，正方形ABCD的對角線AC，BD交于點O，將△COD繞點O逆時針旋轉得到△EOF（旋轉角為銳角），連接AE，BF，DF，則AE=BF．
（1）如圖2，若（1）中的正方形為矩形，其他條件不變．
①探究AE與BF的數量關系，并證明你的結論；
②若BD=7，AE=4，求DF的長；2
（2）如圖3，若（1）中的正方形為平行四邊形，其他條件不變，且BD=10，AC=6，AE=5，請直接寫出DF的長．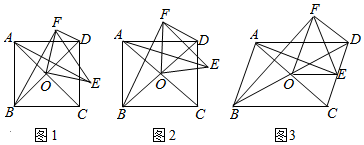
發布：2025/5/25 7:0:2組卷：470引用：4難度：0.3 -
2．△ABC中，∠BAC=60°，AB=AC，點D為直線BC上一動點（點D不與B，C重合），以AD為邊在AD右側作菱形ADEF，使∠DAF=60°，連接CF．
（1）觀察猜想：如圖1，當點D在線段BC上時，
①AB與CF的位置關系為：．
②BC，CD，CF之間的數量關系為：；
（2）數學思考：如圖2，當點D在線段CB的延長線上時，結論①，②是否仍然成立？若成立，請給予證明；若不成立，請你寫出正確結論再給予證明．
（3）拓展延伸：如圖3，當點D在線段BC的延長線上時，設AD與CF相交于點G，若已知AB=4，CD=AB，求AG的長．12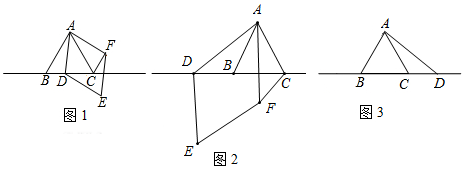
發布：2025/5/25 7:0:2組卷：432引用：4難度：0.1 -
3．利用“平行+垂直”作延長線或借助“平行+角平分線”構造等腰三角形是我們解決幾何問題的常用方法．
（1）發現：
如圖1，AB∥CD，CB平分∠ACD，求證：△ABC是等腰三角形．
（2）探究：
如圖2，AD∥BC，BD平分∠ABC，BD⊥CD于D，若BC=6，求AB．
（3）應用：
如圖3，在?ABCD中，點E在AD上，且BE平分∠ABC，過點E作EF⊥BE交BC的延長線于點F，交CD于點M，延長AB到N使BN=DM，若AD=7，CF=3，tan∠EBF=3，求MN．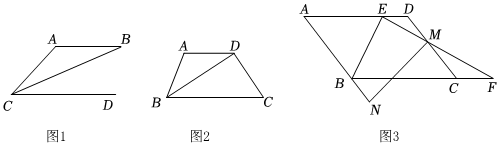
發布：2025/5/25 7:0:2組卷：105引用：1難度：0.2