在矩形ABCD中，AD=2AB=16，點(diǎn)P、Q分別為對角線AC上兩點(diǎn)，且PQ=35，分別過P、Q兩點(diǎn)作PE⊥BC，QF⊥AD，垂足為E、F．
（1）求PE+QF的值；
（2）把△PEQ沿PQ翻折得到△PGQ，當(dāng)點(diǎn)G落在AD邊上時(shí)，求∠PQE的度數(shù)；
（3）在（2）的條件下，把△PGQ繞著點(diǎn)G旋轉(zhuǎn)，得到△MGN，當(dāng)M落在AG邊上時(shí)，設(shè)MN、GN分別AC于R、K，求KR的長．
5
【考點(diǎn)】四邊形綜合題．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：65引用：1難度：0.1
相似題
-
1．已知，正方形ABCD中，∠MAN=45°，∠MAN繞點(diǎn)A順時(shí)針旋轉(zhuǎn)，它的兩邊分別交CB，DC（或它們的延長線）于點(diǎn)M，N，AH⊥MN于點(diǎn)H．
（1）如圖①，當(dāng)∠MAN繞點(diǎn)A旋轉(zhuǎn)到BM=DN時(shí)，請你直接寫出AH與AB的數(shù)量關(guān)系：．
（2）如圖②，當(dāng)∠MAN繞點(diǎn)A旋轉(zhuǎn)到BM≠DN時(shí)，（1）中發(fā)現(xiàn)的AH與AB的數(shù)量關(guān)系還成立嗎？如果不成立請寫出理由，如果成立請證明；
（3）如圖③，已知∠MAN=45°，AH⊥MN于點(diǎn)H，且MH=2，NH=3，探求AH滿足的數(shù)量關(guān)系．（可利用（2）得到的結(jié)論）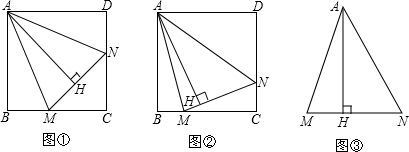
發(fā)布：2025/6/17 11:30:1組卷：879引用：1難度：0.3 -
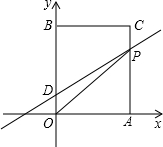2．如圖在平面直角坐標(biāo)系中，O是坐標(biāo)原點(diǎn)，矩形OACB的頂點(diǎn)A，B分別在x軸、y軸上，已知OA=3，點(diǎn)D為y軸上一點(diǎn)，其坐標(biāo)為（0，1），若連接CD，則CD=5，點(diǎn)P從點(diǎn)A出發(fā)以每秒1個(gè)單位的速度沿線段A-C-B的方向運(yùn)動，當(dāng)點(diǎn)P與點(diǎn)B重合時(shí)停止運(yùn)動，運(yùn)動時(shí)間為t秒
（1）求B，C兩點(diǎn)坐標(biāo)；
（2）求△OPD的面積S關(guān)于t的函數(shù)關(guān)系式；
（3）當(dāng)點(diǎn)D關(guān)于OP的對稱點(diǎn)E落在x軸上時(shí)，請直接寫出點(diǎn)E的坐標(biāo)，并求出此時(shí)的t值．發(fā)布：2025/6/17 10:30:2組卷：135引用：3難度：0.1 -
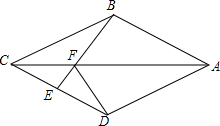3．如圖，在四邊形ABCD中，AB=AD，CB=CD，E是CD上一點(diǎn)，BE交AC于F，連接DF．
（1）證明：∠BAC=∠DAC，∠AFD=∠CFE；
（2）若AB∥CD，試證明四邊形ABCD是菱形；
（3）在（2）的條件下，若BE⊥CD，試證明∠EFD=∠BCD．發(fā)布：2025/6/18 8:30:2組卷：215引用：3難度：0.1