古希臘數學家帕普斯提出著名的蜂窩猜想，認為蜂窩的優美形狀，是自然界最有效勞動的代表．他在《匯編》一書中對蜂房的結構作出精彩的描寫“蜂房是由許許多多的正六棱柱組成，一個挨著一個，緊密地排列，沒有一點空隙．蜜蜂憑著自己本能的智慧選擇了正六邊形，因為使用同樣多的原材料，正六邊形具有最大的面積，從而可貯藏更多的蜂蜜．”某興趣小組以蜂窩為創意來源，制作了幾個棱長均相等的正六棱柱模型，設該正六棱柱的體積為V1，其外接球的體積為V2，則V1V2=（ ）
V
1
V
2
【考點】棱柱、棱錐、棱臺的體積；球的體積和表面積．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 14:0:0組卷：79引用：1難度：0.6
相似題
-
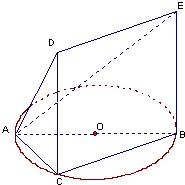1．如圖，△ABC內接于圓O，AB是圓O的直徑，AB=2，BC=1，設AE與平面ABC所成的角為θ，且tanθ=，四邊形DCBE為平行四邊形，DC⊥平面ABC．32
（1）求三棱錐C-ABE的體積；
（2）證明：平面ACD⊥平面ADE；
（3）在CD上是否存在一點M，使得MO∥平面ADE？證明你的結論．發布：2025/1/20 8:0:1組卷：95引用：3難度：0.1 -
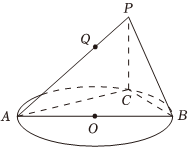2．如圖所示，AB為圓O的直徑，PC⊥平面ABC，Q在線段PA上．
（1）求證：平面BCQ⊥平面ACQ；
（2）若Q為靠近P的一個三等分點，PC=BC=1，，求VP-BCQ的值．AC=22發布：2025/1/20 8:0:1組卷：38引用：3難度：0.6 -
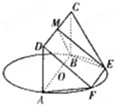3．如圖，AB為圓O的直徑，點E、F在圓O上，AB∥EF，矩形ABCD的邊BC垂直于圓O所在的平面，且AB=2，AD=EF=1．
（Ⅰ）設CD的中點為M，求證：EM∥平面DAF；
（Ⅱ）求三棱錐B-CME的體積．發布：2025/1/20 8:0:1組卷：16引用：1難度：0.5