【教材呈現】如下是華師版八年級下冊數學教材117頁的部分內容．
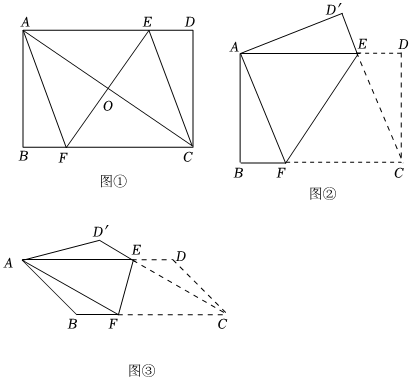
已知：如圖①，已知矩形ABCD的對角線AC的垂直平分線與邊AD、BC分別交于點E、F，求證：四邊形AFCE是菱形．
分析：要證四邊形AFCE是菱形，由已知條件可知EF⊥AC，所以只需證明四邊形AFCE是平行四邊形，又知EF垂直平分AC，所以只需證明OE=OF．
【問題解決】請結合圖①寫出證明過程；
【應用】如圖②，直線EF分別交矩形紙片ABCD的邊AD、BC于點E、F，將矩形紙片ABCD沿著EF翻折，使點C與點A重合，點D與點D'重合，連結CE，若AB=3，BC=4，則EF=154154；
【拓展】如圖③，直線EF分別交平行四邊形ABCD的邊AD、BC于點E、F，將平行四邊形ABCD沿著EF翻折，使點A與點C重合，點D與點D'重合，連結CE，若AB=32，BC=6，∠BCD=45°，則四邊形AFCE的面積是 1515．
15
4
15
4
AB
=
3
2
【考點】四邊形綜合題．
【答案】；15
15
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：271引用：2難度：0.1
相似題
-
1．如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角平分線CF于點F．
（1）求證：AE=EF；
（2）如圖2，若把條件“點E是邊BC的中點”改為“點E是邊BC上的任意一點”，其余條件不變，（1）中的結論是否仍然成立？；（填“成立”或“不成立”）；
（3）如圖3，若把條件“點E是邊BC的中點”改為“點E是邊BC延長線上的一點”，其余條件仍不變，那么結論AE=EF是否成立呢？若成立請證明，若不成立說明理由．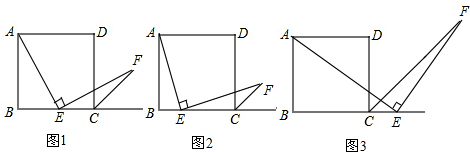
發布：2025/6/8 3:0:2組卷：677引用：7難度：0.5 -
2．如圖1，在正方形ABCD中，點E是BC邊上的一點，∠AEP=90°，且EP交正方形外角的平分線CP于點P．
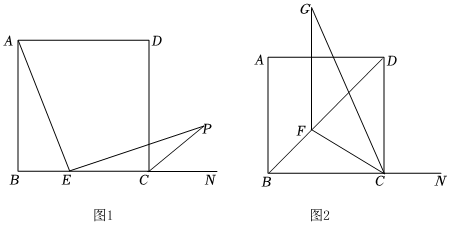
（1）求∠ECP的度數；
（2）求證：AE=EP；
（3）在AB邊上是否存在點M，使得四邊形DEPM是平行四邊形？若存在，請畫出圖形并給予證明；若不存在，請說明理由；
（4）如圖2，在邊長為4的正方形ABCD中，將線段AB沿射線BD平移，得到線段GF，連接CG、CF則直接寫出CF+CG的最小值是 ．發布：2025/6/8 3:30:1組卷：41引用：1難度：0.2 -
3．在平面直角坐標系xOy中，已知，點A（a,0），M（b,a），其中a,b滿足
，9-3b=12a-a2-36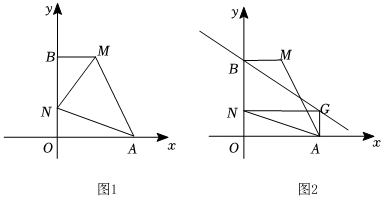
（1）請直接寫出a,b的值；
（2）如圖1，過點M作MB⊥y軸于點B，N為y軸上一點，且∠MAN=45°，求點N的坐標；
（3）如圖2，在（2）的條件下，已知G為第一象限內一點，∠AGN=90°，當OG的值最大時，
①判斷四邊形OAGN的形狀（不必并說明理由）；
②P是y軸上一點，在直線BG上是否存在點Q，使以B，M，P，Q為頂點的四邊形為平行四邊形？若存在，請求出點Q及對應的點P的坐標；若不存在，請說明理由．發布：2025/6/8 4:0:1組卷：121引用：3難度：0.1