如圖，已知∠xOy=90°，線段AB=25，若點A在oy上滑動，點B隨著線段AB在射線Ox上滑動，（A、B與O不重合），Rt△AOB的內(nèi)切⊙K分別與OA、OB、AB切于點E、F、P．
（1）在上述變化過程中：Rt△AOB的周長，⊙K的半徑，△AOB外接圓的半徑，這幾個量中不會發(fā)生變化的是什么？并簡要說明理由；
（2）當(dāng)AE=15時，求⊙K的半徑r；
（3）設(shè)Rt△AOB的面積為S，BF=x,試求：S與x之間的函數(shù)關(guān)系，并求出S最大時直角邊OA的長．
【考點】圓的綜合題．
【答案】（1）不會發(fā)生變化的是△AOB的外接圓半徑，理由見解答過程；
（2）⊙K的半徑為5；
（3）S=-x2+25x，S最大時直角邊OA的長為．
（2）⊙K的半徑為5；
（3）S=-x2+25x，S最大時直角邊OA的長為
25
2
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：31引用：1難度：0.1
相似題
-
1．對于平面直角坐標(biāo)系xOy中的圖形M，N，給出如下定義：P為圖形M上任意一點，Q為圖形N上任意一點，如果P，Q兩點間的距離有最小值，那么稱這個最小值為圖形M，N間的“閉距離”，記作d（M，N）．特殊地，當(dāng)圖形M與圖形N有公共點時，規(guī)定d（M，N）=0．
已知點A（-2，0），B（0，2），C（2，0），D（0，m）．3
（1）①求d（點O，線段AB）；
②若d（線段CD，直線AB）=1，直接寫出m的值；
（2）⊙O的半徑為r,若d（⊙O，線段AB）≤1，直接寫出r的取值范圍；
（3）若直線y=x+b上存在點E，使d（E，△ABC）＜=1，直接寫出b的取值范圍．3發(fā)布：2025/6/10 1:30:1組卷：525引用：2難度：0.1 -
2．如圖，已知⊙O的半徑為1，P是平面內(nèi)一點．
（1）如圖①，若OP=2，過點P作⊙O的兩條切線PE、PF，切點分別為E、F，連接EF．則∠EPO=°，EF=．
（2）若點M、N是⊙O上兩點，且存在∠MPN=90°，則規(guī)定點P為⊙O的“直角點”．
①如圖②，已知平面內(nèi)有一點D，OD=，試說明點D是⊙O的“直角點”．2
②如圖③，直線y=x-2分別與x軸、y軸相交于點A、B，若線段AB上所有點都是半徑為r的圓的“直角點”，求r的最小值與該圓心的坐標(biāo)．23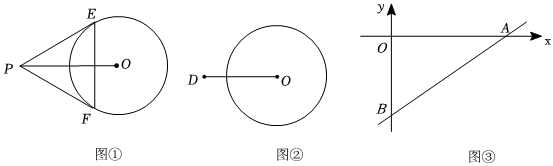
發(fā)布：2025/6/10 0:0:1組卷：215引用：1難度：0.5 -
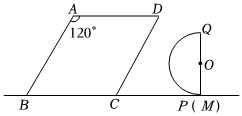3．如圖，在菱形ABCD中，∠A=120°，AB=6，在直線BC上有一點M，CM=5，PQ=4，以PQ為直徑的半圓O與直線BC相切于點P，點N為半圓弧PQ上一動點．
（1）當(dāng)點P與點M重合時，H為半圓O上一點，則線段CH的最小值為 ；
（2）半圓O從點M出發(fā)沿MB做平移運動，速度為每秒1個單位長度，同時點N從點P開始繞圓心順時針旋轉(zhuǎn)，速度為每秒15°，設(shè)運動時間為t秒（0≤t≤11），解決下列問題：
①當(dāng)t=2時，求此時點O到CD的距離及扇形ONP的面積；
②當(dāng)半圓O與菱形ABCD有交點時，直接寫出運動時間t的取值范圍．發(fā)布：2025/6/10 0:30:1組卷：43引用：2難度：0.3