當(dāng)已知三角形一邊中點(diǎn)時，我們常通過“倍長中線”來構(gòu)造全等的兩個三角形，從而解決問題．
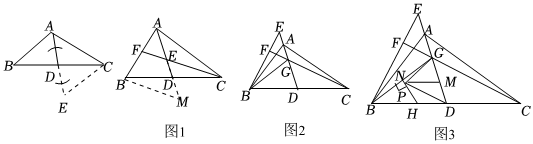
如圖，已知△ABC，點(diǎn)D是BC的中點(diǎn)，延長AD至點(diǎn)E，使DE=AD，連接CE，易得到△ECD≌△ABD，從而得到CE=AB，∠CED=∠BAD．
已知△ABC，點(diǎn)D是BC的中點(diǎn)．
?
（1）如圖1，點(diǎn)E在AD上，延長CE交AB于點(diǎn)F，且FA=FE，求證：CE=AB；小明同學(xué)應(yīng)用倍長中線的方法，延長ED至點(diǎn)M，使ED=DM，連接BM，請你幫助他寫出證明過程；
（2）如圖2，點(diǎn)E，G在射線DA上，連接BE，CG，BG，延長CG交BE于點(diǎn)F，若FE=FG，G為ED的中點(diǎn)，求證：BG=BD；
（3）在（2）的條件下，若點(diǎn)M是線段DG的中點(diǎn)，∠DBG=40°，NH垂直平分線段BG，在NH上有一動點(diǎn)P，連接GP，DP，PM，當(dāng)△GPM的周長最小時，求∠DPH的度數(shù)．
【考點(diǎn)】三角形綜合題．
【答案】（1）證明見解析過程；
（2）證明見解析過程；
（3）30°．
（2）證明見解析過程；
（3）30°．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/15 8:0:9組卷：280引用：6難度：0.5
相似題
-
1．如圖1：AC∥EF，AC=EF，AE=BD．
求證：△ABC≌△EDF．
如圖2：DF=CE，AD=BC，∠D=∠C．
求證：△AED≌△BFC．
如圖3：AB=AC，AD=AE，AB⊥AC，AD⊥AE．求證：（1）∠B=∠C，（2）BD=CE．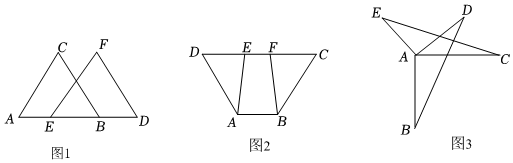
發(fā)布：2025/6/20 4:30:2組卷：11引用：1難度：0.4 -
2．（1）如圖1，已知△ABC，∠ACB=90°，∠ABC=45°，分別以AB，BC為邊向外作△ABD與△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，連接DE交AB于點(diǎn)F．直接寫出線段DF與EF的數(shù)量關(guān)系．
（2）如圖2，若∠ABC=30°，∠ADB=∠BEC=60°，原問題中的其它條件不變，你在（1）中得到的結(jié)論是否發(fā)生變化？請寫出你的猜想，并加以證明；
（3）如圖3，∠ADB=∠BEC=2∠ABC，若原問題中的其他條件不變，你在（1）中得到的結(jié)論是否發(fā)生變化？請寫出你的猜想，并加以證明．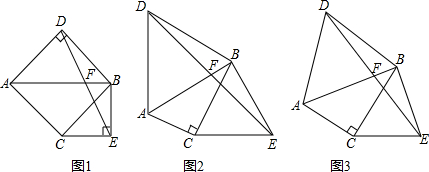
發(fā)布：2025/6/20 2:30:1組卷：109引用：1難度：0.3 -
3．如圖，在等腰直角△ABC中，∠ACB=90°．點(diǎn)P在線段BC上，延長BC至點(diǎn)Q，使得CQ=CP，連接AP，AQ．過點(diǎn)B作BD⊥AQ于點(diǎn)D，交AP于點(diǎn)E，交AC于點(diǎn)F．K是線段AD上的一個動點(diǎn)（與點(diǎn)A，D不重合），過點(diǎn)K作GN⊥AP于點(diǎn)H，交AB于點(diǎn)G，交AC于點(diǎn)M，交FD的延長線于點(diǎn)N．
（1）依題意補(bǔ)全圖1；
（2）求證：NM=NF；
（3）若AM=CP，用等式表示線段AE，GN與BN之間的數(shù)量關(guān)系，并證明．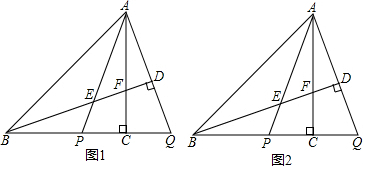
發(fā)布：2025/6/20 3:30:1組卷：1341引用：5難度：0.2