綜合與實踐——探究正方形旋轉中的數學問題．
問程情境：
已知正方形ABCD中，點O是線段BC的中點，將正方形ABCD繞點O順時針旋轉得到正方形A'B'C'D'（點A'，B'，C'，D'分別是點A，B，C，D的對應點）．同學們通過小組合作，提出下列數學問題，請你解答．
特例分析：
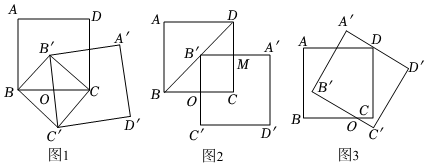
（1）“樂思”小組提出問題：如圖1，在正方形繞點O旋轉過程中，順次連接點B，B'，C，C'得到四邊形BB'CC'，求證：四邊形BB'CC'是矩形；
（2）“善學”小組提出問題：如圖2．在旋轉過程中，當點B'落在對角線BD上時，設A'B'與CD交于點M．求證：四邊形OB'MC是正方形．
深入探究：
（3）“好問”小組提出問題：如圖3．若點O是線段BC的三等分點且OB=2OC，在正方形ABCD旋轉的過程中，當線段A'D'經過點D時，請直接寫出DD′OC′的值．
D
D
′
OC
′
【考點】四邊形綜合題．
【答案】（1）見解析；
（2）見解析；
（3）=2．
（2）見解析；
（3）
DD
′
OC
′
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/3 8:0:9組卷：219引用：4難度：0.3
相似題
-
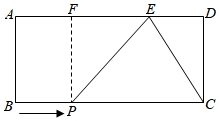1．如圖，矩形ABCD中，AB=4，AD=8，E在AD上，DE=3，點P從點B出發，以每秒1個單位長度的速度沿著BC邊向終點C運動，連接PE，設點P運動的時間為t秒．
（1）過P作PF⊥AD，垂足為F，用含t的式子表示：EF=，PC=；
（2）當t=2時，判斷△PEC是否是直角三角形，并說明理由；
（3）當∠PEC=∠DEC時，求t的值．發布：2025/6/8 12:30:1組卷：43引用：3難度：0.4 -
2．如圖，在正方形ABCD中，AB=BC=CD=AD=6，∠A=∠B=∠BCD=∠ADC=90°，將一直角三角板放在正方形ABCD上，使三角板的直角頂點與D點重合，三角板的一邊交AB于點P，另一邊交BC的延長線于點Q，如圖1所示．
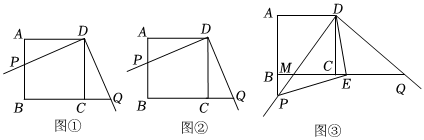
（1）求證：DP=DQ；
（2）如圖2，在圖1的基礎上作∠PDQ的平分線DE交BC于點E，連接PE，請你猜想PE和QE存在何種數量關系，并予以證明；
（3）如圖3，固定三角板直角頂點在D點不動，轉動三角板使三角板的一邊交AB的延長線于點P，另一邊交BC的延長線于點Q，仍作∠PDQ的平分線DE交BC的延長線于點E，連接PE，若BP=2，求△DCE的面積．發布：2025/6/8 12:30:1組卷：58引用：1難度：0.2 -
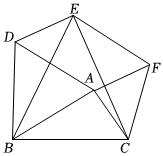3．（1）感知：如圖，分別以△ABC的三邊為邊長，在BC邊的同側分別作三個等邊三角形，即△ABD，△BCE，△ACF，連接DE、EF，試猜想四邊形ADEF的形狀，并證明你的猜想．
（2）應用：當△ABC中有AB=AC時，四邊形ADEF的形狀是 ．
（3）探究：①四邊形ADEF是否隨著△ABC形狀的改變而永遠存在，簡要說明理由；
②如果四邊形ADEF是正方形，則△ABC應滿足什么條件？
（4）若AB=4，AC=3，BC=5，求四邊形AFED的面積．發布：2025/6/8 12:30:1組卷：66引用：2難度：0.3