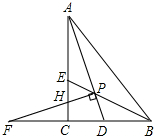
如圖，Rt△ACB中，∠ACB=90°，△ABC的角平分線AD、BE相交于點P，過P作PF⊥AD交BC的延長線于點F，交AC于點H．
（1）求∠APB的度數為 135°135°；
（2）證明：AH+BD=AB．
【考點】全等三角形的判定與性質．
【答案】135°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：473引用：3難度：0.5
相似題
-
1．如圖，AD、CF分別是△ABC的高和角平分線，AD與CF相交于G，AE平分∠CAD交BC于E，交CF于M，連接BM交AD于H，且BM⊥AE．有下列結論：①∠AMC=135°；②△AMH≌△BME；③BC=BH+2MH；④AH+CE=AC．其中，正確的結論有 ．（填序號）發布：2025/5/30 18:30:2組卷：170引用：2難度：0.6 -
2．如圖1，點P、Q分別是邊長為5cm的等邊△ABC邊AB、BC上的動點，點P從頂點A，點Q從頂點B同時出發，且它們的速度都為1cm/s.
（1）連接AQ、CP交于點M，則在P、Q運動的過程中，∠CMQ變化嗎？若變化，則說明理由，若不變，則求出它的度數；
（2）何時△PBQ是直角三角形，求t的值？
（3）如圖2，若點P、Q在運動到終點后繼續在射線AB、BC上運動，直線AQ、CP交點為M，則∠CMQ變化嗎？若變化，則說明理由，若不變，直接寫出它的度數．
發布：2025/5/30 18:30:2組卷：145引用：1難度：0.5 -
3．已知：如圖，∠B=∠C=90°，AF=DE，BE=CF．
求證：AB=DC．發布：2025/5/30 18:30:2組卷：170引用：11難度：0.5