如圖，在△ABC中，∠B=30°，∠C=70°，AE⊥BC于E，AD平分∠BAC，
（1）求∠DAE的度數(shù)；
（2）如圖②，若把“AE⊥BC”變成“點F在DA的延長線上，F(xiàn)E⊥BC”，其他條件不變，求∠DFE的度數(shù)；
（3）如圖③，若把∠B=30°，∠C=70°，AE⊥BC改為“∠C＞∠B，EF⊥BC”，其他條件不變，你能直接寫出∠DFE與∠C，∠B之間的數(shù)量關(guān)系嗎？
?
【考點】幾何變換綜合題．
【答案】（1）20°；
（2）20°；
（3）∠DFE=∠C-∠B．
（2）20°；
（3）∠DFE=
1
2
1
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/13 8:0:9組卷：81引用：1難度：0.2
相似題
-
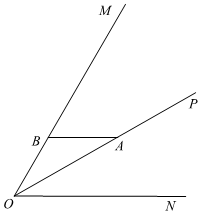1．如圖，已知∠MON=α（0°＜α＜90°），OP是∠MON的平分線，A，B分別在OP，OM上，且AB∥ON．以點A為中心，將線段AO旋轉(zhuǎn)到AC處，使點O的對應(yīng)點C恰好在射線BM上，在射線ON上取一點D，使得∠BAD=180°-α．
（1）①依題意補(bǔ)全圖；
②求證：OC=OD+AD；
（2）連接CD，若CD=OD，求α的度數(shù)，并直接寫出的值．ADOD發(fā)布：2025/6/20 3:30:1組卷：417引用：5難度：0.1 -
2．圖1是邊長分別為a和b（a＞b）的兩個等邊三角形紙片△ABC和△CDE疊放在一起（C與C′重合）的圖形．
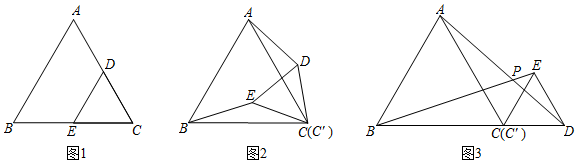
（1）操作：固定△ABC，將△CDE繞點C按順時針方向旋轉(zhuǎn)20°，連結(jié)AD，BE，如圖2，則可證△CBE≌△CAD，依據(jù) ，進(jìn)而得到線段BE=AD，依據(jù) ．
（2）操作：若將圖1中的△CDE，繞點C按順時針方向旋轉(zhuǎn)120°，使點B、C、D在同一條直線上，連結(jié)AD、BE，如圖3．
①線段BE與AD之間是否仍存在（1）中的結(jié)論？若是，請證明；若不是，請直接寫出BE與AD之間的數(shù)量關(guān)系；
②求∠APB的度數(shù)．
（3）若將圖1中的△CDE，繞點C按逆時針方向旋轉(zhuǎn)一個角度α（0＜α＜360°），當(dāng)α等于多少度時，△BCD的面積最大？請直接寫出答案．發(fā)布：2025/6/20 9:30:2組卷：776引用：7難度：0.3 -
3．[實踐與探究]
將△ABC（AB＞AC）沿AD折疊，使點C剛好落在AB邊上的點E處，展開如圖．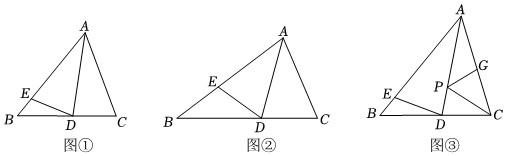
[操作觀察]圖①中，AB=8，AC=6．
①BE=．
②若△ACD的面積是9，則△ABD的面積是 ．
[理解應(yīng)用]如圖②，若∠C=2∠B，試說明：AB=AC+CD．
[拓展延伸]如圖③，若∠BAC=60°，點G為AC的中點，且AG=5．點P是AD上的一個動點，連結(jié)PG、PC，直接寫出（PG+PC）2的最小值．發(fā)布：2025/6/20 8:0:2組卷：64引用：2難度：0.2