如何通過代數推理證明反比例函數圖象的性質?
代數推理指從一定條件出發,依據代數的定義、公式、運算法則、等式的性質、不等式的性質等證明已知結果或結論.
我們不妨來試試
(1)性質:反比例函數y=3x的圖象是中心對稱圖形,對稱中心是原點.
證:在函數上任取一點A(x,3x),
則點A關于原點對稱的點B為( -x-x,-3x-3x),
∵(-x)?(-3x)=3(-x)?(-3x)=3,
∴點B也在反比例函數y=3x的圖象上,
∵點A是反比例函數y=3x上的任意一點,它關于原點對稱的點都在反比例函數y=3x的圖象上,
∴反比例函數y=3x的圖象是中心對稱圖形,對稱中心是原點.
仿照上述方法,嘗試證明
(2)性質:反比例函數y=3x的圖象關于直線y=x對稱,關于直線y=-x對稱.
運用代數推理進行證明
(3)證明:對于反比例函數y=3x,當x>0時,y隨x的增大而減小.
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
【答案】-x;-;(-x)?(-)=3
3
x
3
x
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/7 8:0:9組卷:874引用:2難度:0.6
相似題
-
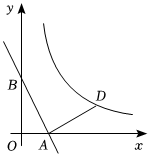 1.如圖,直線y=-2x+2與x軸、y軸分別相交于點A,B兩點,將線段AB繞著點A按順時針方向旋轉90°,點B恰好落在反比例函數在第一象限圖象上的點D.則k=.y=kx發布:2025/5/24 7:30:1組卷:252引用:2難度:0.5
1.如圖,直線y=-2x+2與x軸、y軸分別相交于點A,B兩點,將線段AB繞著點A按順時針方向旋轉90°,點B恰好落在反比例函數在第一象限圖象上的點D.則k=.y=kx發布:2025/5/24 7:30:1組卷:252引用:2難度:0.5 -
2.若點A(-3,y1),B(-2,y2),C(2,y3)都在反比例函數
的圖象上,則y1,y2,y3的大小關系為( )y=-12xA.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1 發布:2025/5/24 7:30:1組卷:158引用:2難度:0.7 -
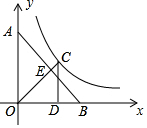 3.如圖,點A,點B分別在y軸,x軸上,OA=OB,點E為AB的中點,連接OE并延長交反比例函數y=(x>0)的圖象于點C,過點C作CD⊥x軸于點D,點D關于直線AB的對稱點恰好在反比例函數圖象上,則OE-EC=.1x發布:2025/5/24 9:0:1組卷:3336引用:16難度:0.5
3.如圖,點A,點B分別在y軸,x軸上,OA=OB,點E為AB的中點,連接OE并延長交反比例函數y=(x>0)的圖象于點C,過點C作CD⊥x軸于點D,點D關于直線AB的對稱點恰好在反比例函數圖象上,則OE-EC=.1x發布:2025/5/24 9:0:1組卷:3336引用:16難度:0.5


